题目内容
8.已知反比例函数y=$\frac{1}{x}$的图象与一次函数y=x-2$\sqrt{3}$的图象相交于点P(a,b),则 $\frac{1}{a}$-$\frac{1}{b}$=-2$\sqrt{3}$.分析 先把两个解析式联立成方程组,得出其交点坐标,再代入代数式即可.
解答 解:因为反比例函数y=$\frac{1}{x}$的图象与一次函数y=x-2$\sqrt{3}$的图象相交于点P(a,b),
所以可得:$\left\{\begin{array}{l}{y=\frac{1}{x}}\\{y=x-2\sqrt{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\sqrt{3}+2}\\{y=2-\sqrt{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\sqrt{3}-2}\\{y=-2-\sqrt{3}}\end{array}\right.$,
把两个方程组的解代入代数式得:$\frac{1}{a}-\frac{1}{b}=\frac{b-a}{ab}=-2\sqrt{3}$,
故答案为:-2$\sqrt{3}$
点评 此题考查反比例函数和一次函数的交点,关键是根据解析式列出方程组解答.

练习册系列答案
相关题目
18.如图,∠1和∠2是同位角的是( )
| A. | 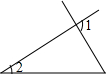 | B. | 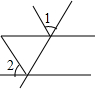 | C. | 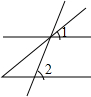 | D. | 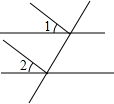 |
20.下列各式计算结果中正确的是( )
| A. | a2+a2=a4 | B. | (-2x2)2=-4x4 | C. | (a+1)2=a2+1 | D. | a•a=a2 |
17.在?ABCD中,对角线AC与BD相交于点O,若AC=8,BD=6,则边长AB的取值范围是( )
| A. | 1<AB<7 | B. | 2<AB<14 | C. | 6<AB<8 | D. | 3<AB<4 |
18.李老师给出:(a-b)2=5,a2+b2=2,你能计算出ab的值为( )
| A. | -1 | B. | 3 | C. | -$\frac{3}{2}$ | D. | -$\frac{1}{2}$ |
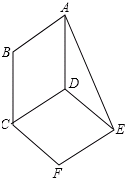 如图,平行四边形ABCD与平行四边形DCFE的周长相等,且∠BAD=60°,∠F=110°,BC=6.
如图,平行四边形ABCD与平行四边形DCFE的周长相等,且∠BAD=60°,∠F=110°,BC=6. 在4×4的方格中有五个同样大小的正方形按图示位置摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法有( )个.
在4×4的方格中有五个同样大小的正方形按图示位置摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法有( )个.