题目内容
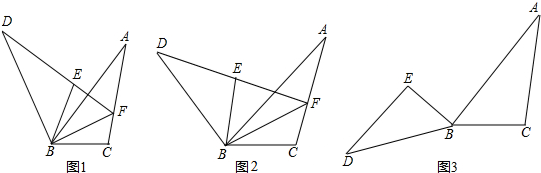
将△ABC绕点B逆时针旋转α(0°<α<180°)得到△DBE,直线DE与直线AC相交于点F,连接BF.
(1)如图1,若α=60°,DF=2AF,请直接写
等于 ;
(2)若DF=mAF,(m>0,且m≠1)
①如图2,求
;(用含α,m的式子表示)
②如图3,依题意补全图形,请直接写出
等于 .(用含α,m的式子表示)
(1)如图1,若α=60°,DF=2AF,请直接写
| AF |
| BF |
(2)若DF=mAF,(m>0,且m≠1)
①如图2,求
| AF |
| BF |
②如图3,依题意补全图形,请直接写出
| AF |
| BF |

考点:几何变换综合题
专题:
分析:(1)连接AD,G是DF的中点,连接AG,然后证得△ABD和△AGF是等边三角形,再证得△BDF≌△ADF,得出BF=AF即可求得;
(2)①在DF上截取DG=AF,连接BG,由旋转知,DB=AB,∠D=∠A,从而证得△DBG≌△ABF,然后通过解直角三角形即可求得;
②延长FD到G,使DG=AF,连接BG,先证得△DBG≌△ABF,然后解直角三角形即可求得;
(2)①在DF上截取DG=AF,连接BG,由旋转知,DB=AB,∠D=∠A,从而证得△DBG≌△ABF,然后通过解直角三角形即可求得;
②延长FD到G,使DG=AF,连接BG,先证得△DBG≌△ABF,然后解直角三角形即可求得;
解答:解:(1)连接AD,G是DF的中点,连接AG,
∵∠BAC=∠BDE,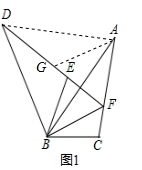
∴∠ABD=∠AFG=60°,
∵DF=2AF,
∴AF=GF,
∴AG=AF=GF=DG,
∴∠ADG=∠DAG=30°,
∵AB=DB,∠ABD=60°,
∴△ABD是等边三角形,
∴∠ABD=60°,BD=AD,
∴∠ADF=∠BDF=30°,
在△BDF与△ADF中
∴△BDF≌△ADF(SAS),
∴AF=BF,
∴
=1.
故答案为1.
(2)①如图2,在DF上截取DG=AF,连接BG,
由旋转知,DB=AB,∠D=∠A,
在△DBG与△ABF中
∴△DBG≌△ABF(SAS),
∴BG=BF,∠GBF=α,
过点B作BN⊥GF于点N,
∴点N为GF中点,∠FBN=
,
在RT△BNF中,NF=BF•sin
,
∴GF=2BF•sin
,
∵DF=DG+GF,
∴mAF=AF+2BF•sin
,
∴(m-1)AF=2BF•sin
,
∴
=
sin
.
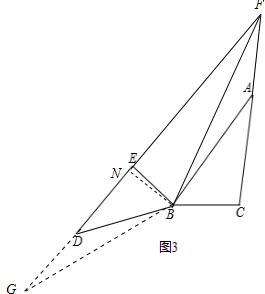
②如图3,依题意补全的图形,
延长FD到G,使DG=AF,连接BG,
由旋转知,DB=AB,∠BDG=∠BAF,
∴△DBG≌△ABF(SAS),
∴BG=BF,∠GBF=α,
过点B作BN⊥GF于点N,
∴点N为GF中点,∠FBN=
,
在RT△BNF中,NF=BF•sin
,
∴GF=2BF•sin
,
∵GF=GD+DF,
∴2BF•sin
=AF+mAF,
∴2BF•sin=(m+1)AF,
∴
=
sin
,
故答案为
sin
.
∵∠BAC=∠BDE,

∴∠ABD=∠AFG=60°,
∵DF=2AF,
∴AF=GF,
∴AG=AF=GF=DG,
∴∠ADG=∠DAG=30°,
∵AB=DB,∠ABD=60°,
∴△ABD是等边三角形,
∴∠ABD=60°,BD=AD,
∴∠ADF=∠BDF=30°,
在△BDF与△ADF中
|
∴△BDF≌△ADF(SAS),
∴AF=BF,
∴
| AF |
| BF |
故答案为1.
(2)①如图2,在DF上截取DG=AF,连接BG,

由旋转知,DB=AB,∠D=∠A,
在△DBG与△ABF中
|
∴△DBG≌△ABF(SAS),
∴BG=BF,∠GBF=α,
过点B作BN⊥GF于点N,
∴点N为GF中点,∠FBN=
| α |
| 2 |
在RT△BNF中,NF=BF•sin
| α |
| 2 |
∴GF=2BF•sin
| α |
| 2 |
∵DF=DG+GF,
∴mAF=AF+2BF•sin
| α |
| 2 |
∴(m-1)AF=2BF•sin
| α |
| 2 |
∴
| AF |
| BF |
| 2 |
| m-1 |
| α |
| 2 |

②如图3,依题意补全的图形,
延长FD到G,使DG=AF,连接BG,
由旋转知,DB=AB,∠BDG=∠BAF,
∴△DBG≌△ABF(SAS),
∴BG=BF,∠GBF=α,
过点B作BN⊥GF于点N,
∴点N为GF中点,∠FBN=
| α |
| 2 |
在RT△BNF中,NF=BF•sin
| α |
| 2 |
∴GF=2BF•sin
| α |
| 2 |
∵GF=GD+DF,
∴2BF•sin
| α |
| 2 |
∴2BF•sin=(m+1)AF,
∴
| AF |
| BF |
| 2 |
| m+1 |
| α |
| 2 |
故答案为
| 2 |
| m+1 |
| α |
| 2 |
点评:本题考查了旋转的性质,等边三角形的判定和性质,三角形全等的判定和性质,应用直角三角函数解直角三角形等,本题的根据是构建直角三角形,通过解直角三角形求得结果.

练习册系列答案
相关题目

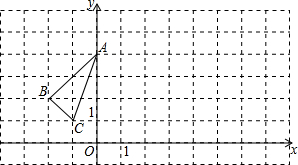 如图,已知在平面直角坐标系中,△ABC的位置如图.
如图,已知在平面直角坐标系中,△ABC的位置如图.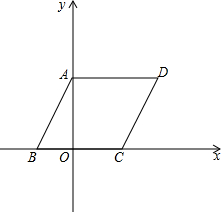 如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.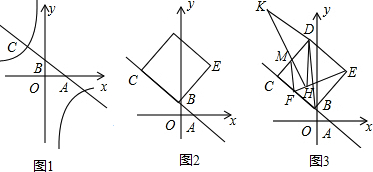
 如图,已知点A和点B是直线y=
如图,已知点A和点B是直线y=