题目内容
如图1,直线y=-
x+1交x轴于点A,交y轴于点B,C(m,-m)是直线AB上一点,双曲线y=
经过C点.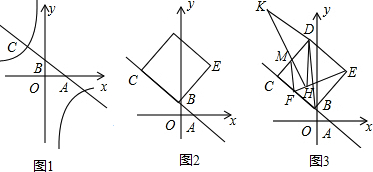
(1)求点C的坐标及双曲线的解析式.
(2)如图2,以CB为边在直线AB的上方作正方形BCDE,求点D的坐标,并判断点D是否在(1)中所求双曲线上?
(3)如图3,M,F分别是正方形BCDE的边CD,BC上的点,且MF∥BD,在ED的延长线上取一点K,使得DK=DE,KM与EF相交于点H,证明:∠EDH=2∠BEF.
| 1 |
| 2 |
| k |
| x |

(1)求点C的坐标及双曲线的解析式.
(2)如图2,以CB为边在直线AB的上方作正方形BCDE,求点D的坐标,并判断点D是否在(1)中所求双曲线上?
(3)如图3,M,F分别是正方形BCDE的边CD,BC上的点,且MF∥BD,在ED的延长线上取一点K,使得DK=DE,KM与EF相交于点H,证明:∠EDH=2∠BEF.
考点:反比例函数综合题
专题:
分析:(1)把C的坐标代入一次函数的解析式,即可得到一个关于m的方程,解得m的值,即可得到C的坐标,然后利用待定系数法求得函数的解析式;
(2)作CM⊥y轴于点M,DN⊥y轴于点N,DF⊥CM于点F,然后证明△CDF≌△BCM,即可求得D的坐标,代入双曲线的解析式即可判断;
(3)证明△KDM≌△EBF,证得∠KMD=∠EFB,然后证明△KHE是直角三角形,根据直角三角形的斜边的中线等于斜边的一半,利用等边对等角,以及三角形的外角的性质即可证得.
(2)作CM⊥y轴于点M,DN⊥y轴于点N,DF⊥CM于点F,然后证明△CDF≌△BCM,即可求得D的坐标,代入双曲线的解析式即可判断;
(3)证明△KDM≌△EBF,证得∠KMD=∠EFB,然后证明△KHE是直角三角形,根据直角三角形的斜边的中线等于斜边的一半,利用等边对等角,以及三角形的外角的性质即可证得.
解答:解:(1)把x=m,y=-m代入y=-
x+1,得:-m=-
m+1,
解得:m=-2,
则C的坐标是(-2,2),
代入y=
得:k=-4,
则双曲线的解析式是:y=-
;
(2)在y=-
x+1中,令x=0,解得:y=1,则B的坐标是(0,1).
 作CM⊥y轴于点M,DN⊥y轴于点N,DF⊥CM于点F.
作CM⊥y轴于点M,DN⊥y轴于点N,DF⊥CM于点F.
则CM=2,AM=2,BM=2-1=1.
∵∠DCB=∠DCM+∠MCB=90°,
又∵直角△BCM中,∠MCB+∠CBM=90°,
∴∠DCM=∠CBM,
则在△CDF和△BCM中,
,
∴△CDF≌△BCM,
∴CF=BM=1,DF=CM=2,
∴MN=DF=2,
则AN=4,DN=FM=CM-CF=1,
则D的坐标是(-1,4),
满足y=-
,即D在双曲线上;
(3)∵BCDE是正方形,
∴BC=CD,
又∵MF∥BD,
∴CM=CF,
∴MD=FB,
∴在△KDM和△EBF中,
,
∴△KDM≌△EBF,
∴∠KMD=∠EFB,
∴∠CMH+∠CFH=∠KMD+∠CFH=∠EFB+∠CFH=180°,
又∠MCF=90°,
∴∠MHF=90°,
∴△KHE是直角三角形.
又∵DK=DE,
∴KD=DP,
∴∠K=∠DHP,
又∵∠EDH=∠K+∠DHK,∠KMD=∠EFB,
∴∠EDH=2∠BEF.
| 1 |
| 2 |
| 1 |
| 2 |
解得:m=-2,
则C的坐标是(-2,2),
代入y=
| k |
| x |
则双曲线的解析式是:y=-
| 4 |
| x |
(2)在y=-
| 1 |
| 2 |
 作CM⊥y轴于点M,DN⊥y轴于点N,DF⊥CM于点F.
作CM⊥y轴于点M,DN⊥y轴于点N,DF⊥CM于点F.则CM=2,AM=2,BM=2-1=1.
∵∠DCB=∠DCM+∠MCB=90°,
又∵直角△BCM中,∠MCB+∠CBM=90°,
∴∠DCM=∠CBM,
则在△CDF和△BCM中,
|
∴△CDF≌△BCM,
∴CF=BM=1,DF=CM=2,
∴MN=DF=2,
则AN=4,DN=FM=CM-CF=1,
则D的坐标是(-1,4),
满足y=-
| 4 |
| x |
(3)∵BCDE是正方形,
∴BC=CD,
又∵MF∥BD,
∴CM=CF,
∴MD=FB,
∴在△KDM和△EBF中,
|
∴△KDM≌△EBF,
∴∠KMD=∠EFB,
∴∠CMH+∠CFH=∠KMD+∠CFH=∠EFB+∠CFH=180°,
又∠MCF=90°,
∴∠MHF=90°,
∴△KHE是直角三角形.
又∵DK=DE,
∴KD=DP,
∴∠K=∠DHP,
又∵∠EDH=∠K+∠DHK,∠KMD=∠EFB,
∴∠EDH=2∠BEF.
点评:本题考查了正方形的性质以及待定系数法求函数的解析式,全等三角形的判定与性质,正确求得D的坐标,以及证明△KDM≌△EBF是关键.

练习册系列答案
相关题目
 如图,在△ABC中,AB=AC,中线BD将这个三角形的周长分为15和6两部分,求△ABC的三边的长.
如图,在△ABC中,AB=AC,中线BD将这个三角形的周长分为15和6两部分,求△ABC的三边的长. 如图,在正方形ABCD中,E是对角线BD上的一点,连接AE、CE.求证:AE=CE.
如图,在正方形ABCD中,E是对角线BD上的一点,连接AE、CE.求证:AE=CE.

 将四个长为m,宽为n的长方形拼成如图的正方形,则图中阴影部分的面积可以用两种不同的方法表示,请通过观察写出(m-n)2,(m+n)2,mn之间的等量关系
将四个长为m,宽为n的长方形拼成如图的正方形,则图中阴影部分的面积可以用两种不同的方法表示,请通过观察写出(m-n)2,(m+n)2,mn之间的等量关系 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2).