Question

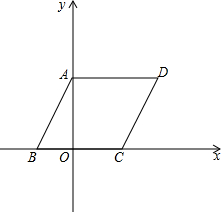如图，在平面直角坐标系中，四边形ABCD是平行四边形，AD=6，若OA、OB的长是关于x的一元二次方程x²-7x+12=0的两个根，且OA＞OB．
（1）求OA、OB的长．
（2）若点E为x轴正半轴上的点，且S_△AOE=

16

3

，求经过D、E两点的直线解析式及经过点D的反比例函数的解析式，并判断△AOE与△AOD是否相似．
（3）若点M在平面直角坐标系内，则在直线AB上是否存在点F，使以A、C、F、M为顶点的四边形为菱形？若存在，直接写出F点的坐标，若不存在，请说明理由．

Answer 1

考点：四边形综合题

专题：综合题

分析：（1）解一元二次方程求出OA，OB的长度即可；
（2）先根据三角形的面积求出点E的坐标，并根据平行四边形的对边相等的性质求出点D的坐标，然后利用待定系数法求解直线的解析式；分别求出两三角形夹直角的两对应边的比，如果相等，则两三角形相似，否则不相似；
（3）根据菱形的性质，分AC与AF是邻边并且点F在射线AB上与射线BA上两种情况，以及AC与AF分别是对角线的情况分别进行求解计算．

解答：解：（1）方程x²-7x+12=0，
分解因式得：（x-3）（x-4）=0，
可得：x-3=0，x-4=0，
解得：x₁=3，x₂=4，
∵OA＞OB，
∴OA=4，OB=3；
（2）根据题意，设E（x，0），则S_△AOE=

1

2

×OA×x=

1

2

×4x=

16

3

，
解得：x=

8

3

，
∴E（

8

3

，0）或（-

8

3

，0），
∵四边形ABCD是平行四边形，
∴点D的坐标是（6，4），
设经过D、E两点的直线的解析式为y=kx+b，
则①

8 3 k+b=0 6k+b=4

，
解得：

k= 6 5 b=- 16 5

，
∴解析式为y=

6

5

x-

16

5

；
②

- 8 3 k+b=0 6k+b=4

，
解得：

k= 6 13 b= 16 13

，
解析式为：y=

6

13

x+

16

13

，
在△AOE与△DAO中，

OA

OE

=

4

8 3

=

3

2

，

AD

OA

=

6

4

=

3

2

，
∴

OA

OE

=

AD

OA

，
又∵∠AOE=∠OAD=90°，
∴△AOE∽△DAO；
（3）根据计算的数据，OB=OC=3，
∵AO⊥BC，
∴AO平分∠BAC，
分四种情况考虑：
①AC、AF是邻边，点F在射线AB上时，AF=AC=5，
∴点F与B重合，即F（-3，0）；
②AC、AF是邻边，点F在射线BA上时，M应在直线AD上，且FC垂直平分AM，
此时点F坐标为（3，8）；
③AC是对角线时，做AC垂直平分线L，AC解析式为y=-

4

3

x+4，直线L过（

3

2

，2），且k值为

3

4

（平面内互相垂直的两条直线k值乘积为-1），
∴L解析式为y=

3

4

x+

7

8

，
联立直线L与直线AB，得：

y= 3 4 x+ 7 8 y= 4 3 x+4

，
解得：x=-

75

14

，y=-

22

7

，
∴F（-

75

14

，-

22

7

）；
④AF是对角线时，过C做AB垂线，垂足为N，
∵S_△ABC=

1

2

BC•OA=

1

2

AB•CN=12，
∴CN=

BC•OA

AB

=

24

5

，
在△BCN中，BC=6，CN=

24

5

，
根据勾股定理得BN=

BC2-CN2

=

18

5

，即AN=AB-BN=5-

18

5

=

7

5

，
做A关于N的对称点，记为F，AF=2AN=

14

5

，
过F做y轴垂线，垂足为G，FG=AFsin∠BAO=

14

5

×

3

5

=

42

25

，
∴F（-

42

25

，

44

25

），
综上所述，满足条件的点有四个：F₁（-3，0）；F₂（3，8）；F₃（-

75

14

，-

22

7

）；F₄（-

42

25

，

44

25

）．

点评：此题考查了解一元二次方程，相似三角形的性质与判定，待定系数法求函数解析式，综合性较强，（3）求点F要根据AC与AF是邻边与对角线的情况进行讨论，不要漏解．