Question

7．如图，在△ABC中，BC的垂直平分线交它的外接圆于D、E两点．若∠B=24°，∠C=106°，则$\widehat{AD}$的度数为82°．

Answer 1

分析 根据垂径定理的推理可判断DE为直径，根据垂径定理得到$\widehat{BE}$=$\widehat{CE}$，设△ABC的外接圆的圆心为O，连结OC、OA，如图，再利用三角形内角和计算出∠BAC=50°，利用圆周角定理得到∠EOC=∠BAC=50°，∠AOC=2∠B=48°，然后计算出∠AOD的度数，再根据$\widehat{AD}$的度数等于它所对的圆心角的度数求解即可．

解答 解：∵DE垂直平分BC，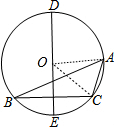
∴DE为直径，$\widehat{BE}$=$\widehat{CE}$，
设△ABC的外接圆的圆心为O，连结OC、OA，如图，
∵∠B=24°，∠C=106°，
∴∠BAC=180°-24°-106°=50°，
∴∠EOC=∠BAC=50°，
∵∠AOC=2∠B=48°，
∴∠AOD=180°-∠COE-∠AOC=180°-50°-48°=82°，
∴$\widehat{AD}$的度数为82°．
故答案为82．

点评 本题考查了三角形的外接圆与外心：三角形外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心．解决本题的关键是把求弧的度数转化为求弧所对的圆心角的度数．