题目内容
8.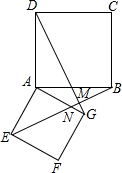 如图,共顶点A的两个正方形ABCD、AEFG,连接DG、BE,且BE交DG于M点,交AG于N点.求证:
如图,共顶点A的两个正方形ABCD、AEFG,连接DG、BE,且BE交DG于M点,交AG于N点.求证:(1)DG=BE;
(2)DG⊥BE.
分析 (1)通过全等三角形(△DAG≌△BAE)的对应边相等证得结论;
(2)利用(1)中全等三角形的对应角相等得到∠DGA=∠AEB,所以在△AEN和△MNG中,利用三角形内角和定理推知∠GMN=90°即可.
解答  证明:(1)∵∠DAB=∠GAE=90°,
证明:(1)∵∠DAB=∠GAE=90°,
∴∠DAB+∠GAB=∠GAE+∠GAB,即:∠DAG=∠BAE,
在△DAG与△BAE中,
$\left\{\begin{array}{l}{DA=AB}\\{∠DAG=∠BAE}\\{AG=AE}\end{array}\right.$,
∴△DAG≌△BAE(SAS),
∴DG=BE;
(2)由(1)知,△DAG≌△BAE,则∠DGA=∠AEB,即MGN=∠AEN,
∵∠ANE=∠GNB,
∴∠NAE=∠GMN=90°,
∴DG⊥BE.
点评 本题考查了全等三角形的判定与性质和正方形的性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
3.下列方程中,有两个不相等的实数根的是( )
| A. | x2+1=0 | B. | x2-2x+1=0 | C. | x2+x+2=0 | D. | x2+2x-1=0 |
13.绿色植物靠吸收光量子来进行光合作用,已知每个光量子的波长约为0.000688毫米,则每个光量子的波长可用科学记数法表示为( )米.
| A. | 6.88×10-4 | B. | 6.88×10-7 | C. | 0.688×10-3 | D. | 0.688×10-6 |
18.在△ABC中,三边长满足b2-a2=c2,则互余的一对角是( )
| A. | ∠A与∠B | B. | ∠B与∠C | C. | ∠A与∠C | D. | 以上都不正确 |
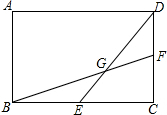 如图,E、F分别是矩形ABCD的边AB、BC的中点,连接CE、AF,设CE、AF相交于点G,则S四边形ABGD:S四边形ABCD=2:3.
如图,E、F分别是矩形ABCD的边AB、BC的中点,连接CE、AF,设CE、AF相交于点G,则S四边形ABGD:S四边形ABCD=2:3.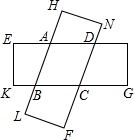 如图,由两个等宽的矩形叠合而得到四边形ABCD.
如图,由两个等宽的矩形叠合而得到四边形ABCD.