题目内容
20.抛物线C1:y=(x-m)2+m+1(m>0)的顶点为A,抛物线C2开口向下且顶点B在y轴上,若A、B两点关于点P(1,2)对称.(1)求m的值;
(2)若抛物线C2与x轴的正半轴的交点是C,当△ABC为直角三角形时,求抛物线C2的解析式.
分析 (1)由C1:y=(x-m)2+m+1(m>0),可求得顶点A(m,m+1),由于点B在y轴上,根据对称即可解得m=2;
(2)由(1)知A(2,3)、B(0,1)根据勾股定理可得AB2=(2-0)2+(3-1)2=8由抛物线C2的顶点B(0,1)在y轴上得到抛物线C2的解析式为y=ax2+1设点C坐标为(c,0),根据勾股定理得到AC2=(2-c)2+32=c2-4c+13;BC2=c2+1由于△ABC是直角三角形,进行分类讨论即可求出结果.
解答 解:(1)∵C1:y=(x-m)2+m+1(m>0)
∴顶点A(m,m+1),
∵点B在y轴上,
∴设B(0,b),
又A、B关于点P(1,2)对称,
∴$\left\{\begin{array}{l}{\frac{0+m}{2}=1}\\{\frac{b+m+1}{2}=2}\end{array}\right.$,解得:m=2;
(2)由(1)知A(2,3)、B(0,1)
∴AB2=(2-0)2+(3-1)2=8
∵抛物线C2的顶点B(0,1)在y轴上
∴抛物线C2的解析式为y=ax2+1
设点C坐标为(c,0),
∴AC2=(2-c)2+32=c2-4c+13;BC2=c2+1
∵△ABC是直角三角形,
则:①当∠ABC=90°时,AC2=BC2+AB2,
即c2-4c+13=(c2+1)+8,解得:c=1
∴C1(1,0),
将点C1坐标代入y=ax2+1得:a+1=0;解得:a=-1,
∴抛物线C2的解析式为:y=-x2+1,
②当∠BAC=90°时,BC2=AC2+AB2,
即c2+1=(c2-4c+13)+8,解得:c=5,
∴C2(5,0),
将点C2坐标代入y=ax2+1得:25a+1=0,解得:a=-$\frac{1}{25}$,
∴抛物线C2的解析式为:y=-$\frac{1}{25}$x2+1,
综上,当△ABC为直角三角形时,抛物线C2的解析式为:y=-x2+1或y=-$\frac{1}{25}$x2+1.
点评 本题考查了抛物线与X轴的交点,关于点对称,正确理解关于点对称是解题的关键.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案| 人数 | 平均身高(单位:厘米) | 方差 | |
| 男生 | 15 | 175 | 36 |
| 女生 | 15 | 165 | 16 |
①两条直线被第三条直线所截,同位角相等
②过一点有且只有一条直线与已知直线垂直
③两个无理数的积一定是无理数
④-$\sqrt{8}$>$\root{3}{-27}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | M(-2,3) | B. | M(-2,-3) | C. | M(2,3) | D. | M(2,-3) |
| A. | 5 | B. | 5$\sqrt{5}$ | C. | 8 | D. | 10$\sqrt{5}$ |
| A. | $\sqrt{9}$ | B. | $\sqrt{7}$ | C. | $\sqrt{20}$ | D. | $\sqrt{\frac{1}{3}}$ |
 尺规作图(不写作法,保留作图痕迹):如图,已知∠AOB及OA边上的点C,过点C作射线CE,使CE∥OB.
尺规作图(不写作法,保留作图痕迹):如图,已知∠AOB及OA边上的点C,过点C作射线CE,使CE∥OB.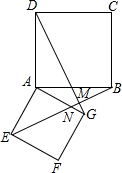 如图,共顶点A的两个正方形ABCD、AEFG,连接DG、BE,且BE交DG于M点,交AG于N点.求证:
如图,共顶点A的两个正方形ABCD、AEFG,连接DG、BE,且BE交DG于M点,交AG于N点.求证: