题目内容
16.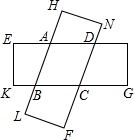 如图,由两个等宽的矩形叠合而得到四边形ABCD.
如图,由两个等宽的矩形叠合而得到四边形ABCD.(1)试判断四边形ABCD的形状并证明.
(2)若矩形长为8cm,宽为2cm,求四边形ABCD的最大面积.
分析 (1)作AR⊥BC于R,AS⊥CD于S,根据题意先证出四边形ABCD是平行四边形,再由BC=CD得平行四边形ABCD是菱形;
(2)设BC=x,则CG=6-x,CD=BC=x,在Rt△CDG中,由勾股定理得出x,再求得面积.
解答 解:(1)四边形ABCD是菱形.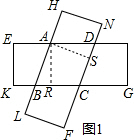
理由:作AR⊥BC于R,AS⊥CD于S,
由题意知:AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∵两个矩形的宽度相等,
∴AR=AS,
∵AR•BC=AS•CD,
∴BC=CD,
∴平行四边形ABCD是菱形;
(2)当这两张纸片叠合成如图2时,菱形的面积最大,
设BC=x,则CG=8-x,CD=BC=x,
在Rt△CBG中,CG2+BG2=BC2,
∴(8-x)2+22=x2,
解得x=$\frac{17}{4}$,
∴S=BG•DG=$\frac{17}{2}$.
点评 本题考查了菱形的判定和性质、勾股定理和矩形的性质等知识点,正确的画出图形是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
14.用两种边长相等的正多边形地砖铺地,已有正方形的地砖,还可选择地砖形状为( )
| A. | 正五边形 | B. | 正六边形 | C. | 正八边形 | D. | 正十边形 |
4.数字0.00000336用科学记数法表示为( )
| A. | 3.36×10-5 | B. | 3.36×10-6 | C. | 33.6×10-5 | D. | 3.36×10-8 |
11.小芸统计了自己班同学的身高,整理分析数据后得到如下结论:
则全班所有同学身高的方差为26.
| 人数 | 平均身高(单位:厘米) | 方差 | |
| 男生 | 15 | 175 | 36 |
| 女生 | 15 | 165 | 16 |
1.在下列四个有理数0,1,$\frac{3}{2}$,2中,与无理数$\sqrt{2}$最接近的是( )
| A. | 0 | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
6.计算${({7^{-1}}-\frac{1}{4})^0}$的结果等于( )
| A. | 0 | B. | 1 | C. | $\frac{1}{4}$ | D. | 没有意义 |
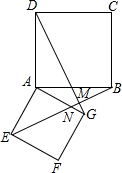 如图,共顶点A的两个正方形ABCD、AEFG,连接DG、BE,且BE交DG于M点,交AG于N点.求证:
如图,共顶点A的两个正方形ABCD、AEFG,连接DG、BE,且BE交DG于M点,交AG于N点.求证: