题目内容
5. 在△ABC中,已知∠B=50°,∠C=60°,AE⊥BC于E,AD平分∠BAC;求:∠DAE的度数.
在△ABC中,已知∠B=50°,∠C=60°,AE⊥BC于E,AD平分∠BAC;求:∠DAE的度数.
分析 先根据三角形内角和定理求出∠BAC的度数,再由角平分线的定义得出∠CAD的度数,根据AE⊥BC于E求出∠CAE的度数,进而可得出结论.
解答 解:∵在△ABC中,∠B=50°,∠C=60°,
∴∠BAC=180°-50°-60°=70°.
∵AD平分∠BAC,
∴∠CAD=$\frac{1}{2}$∠BAC=35°.
∵AE⊥BC于E,
∴∠CAE=90°-60°=30°,
∴∠DAE=∠CAD-∠CAE=35°-30°=5°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
13.下列二次根式不能再化简的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{{x^2}+y}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\sqrt{4{x^2}+16{y^2}}$ |
 如图,DF平分∠CDE,∠CDF=55°,∠C=70°,试判断DE与BC的位置关系并说明理由.
如图,DF平分∠CDE,∠CDF=55°,∠C=70°,试判断DE与BC的位置关系并说明理由. 如图四边形ABCD中,已知AB∥CD,AD∥BC,AE⊥BC于E,AF⊥CD于F,求证:∠BAD+∠EAF=180°.
如图四边形ABCD中,已知AB∥CD,AD∥BC,AE⊥BC于E,AF⊥CD于F,求证:∠BAD+∠EAF=180°. 观察有理数a、b、c在数轴上的位置并去绝对值:
观察有理数a、b、c在数轴上的位置并去绝对值: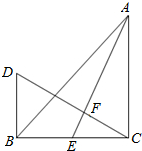 如图,△ABC中,∠ACB=90°,AC=BC,AE是BC上的中线,过C作CF⊥AE,垂足为F点,过B作BD⊥BC交CF的延长线于D点.若BD=3cm,求线段AC的长.
如图,△ABC中,∠ACB=90°,AC=BC,AE是BC上的中线,过C作CF⊥AE,垂足为F点,过B作BD⊥BC交CF的延长线于D点.若BD=3cm,求线段AC的长.