题目内容
8.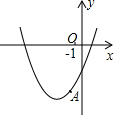 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点A,点(-2,m)和(-5,n)在该抛物线上,则下列结论中不正确的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点A,点(-2,m)和(-5,n)在该抛物线上,则下列结论中不正确的是( )| A. | b2>4ac | B. | m>n | ||
| C. | 方程ax2+bx+c=-4的两根为-5或-1 | D. | ax2+bx+c≥-6 |
分析 由抛物线与x轴有两个交点则可对A进行判断;根据抛物线上的点离对称轴的远近,则可对B进行判断;根据二次函数的对称性可对C进行判断;由于抛物线开口向上,有最小值则可对D进行判断.
解答 解:A、图象与x轴有两个交点,方程ax2+bx+c=0有两个不相等的实数根,b2-4ac>0所以b2>4ac,故A选项正确;
B、抛物线的对称轴为直线x=-3,因为-5离对称轴的距离大于-2离对称轴的距离,所以m<n,故B选项错误;
C、根据抛物线的对称性可知,(-1,-4)关于对称轴的对称点为(-5,-4),所以关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1,故C选项正确.
D、抛物线的开口向上,函数有最小值,因为抛物线的最小值为-6,所以ax2+bx+c≥-6,故D选项正确;
故选B.
点评 本题考查了二次函数图象与系数的关系,二次函数图象上点的坐标特征,抛物线与x轴的交点远近二次函数与不等式的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.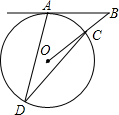 如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=30°,则∠ABO的度数为( )
如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=30°,则∠ABO的度数为( )
 如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=30°,则∠ABO的度数为( )
如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=30°,则∠ABO的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
13.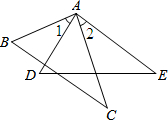 已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )
已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )
 已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )
已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )| A. | AE=AC | B. | ∠B=∠D | C. | BC=DE | D. | ∠C=∠E |
17.八(1)班组织了一次汉字听写比赛,甲、乙两队各10人,其比赛成绩如下表(10分制):
(1)甲队成绩的中位数是9分,乙队成绩的众数是10分.
(2)计算甲队的平均成绩和方差.
(3)已知乙队成绩的方差是1.4,则成绩较为整齐的是甲队.
| 甲队 | 7 | 8 | 9 | 10 | 10 | 10 | 10 | 9 | 9 | 8 |
| 乙队 | 7 | 7 | 8 | 9 | 10 | 10 | 9 | 10 | 10 | 10 |
(2)计算甲队的平均成绩和方差.
(3)已知乙队成绩的方差是1.4,则成绩较为整齐的是甲队.
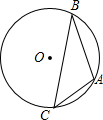 已知:如图,A,B,C为⊙O上的三个点,⊙O的直径为4cm,∠ACB=45°,求AB的长.
已知:如图,A,B,C为⊙O上的三个点,⊙O的直径为4cm,∠ACB=45°,求AB的长. 如图,利用一面足够长的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏),设矩形ABCD的宽AD为x米,矩形的长为AB(且AB>AD).
如图,利用一面足够长的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏),设矩形ABCD的宽AD为x米,矩形的长为AB(且AB>AD).