题目内容
9. 如图,无盖的长方体盒子的长为15,宽为10,高为8,在顶点B处(盒子里面)有一滴蜂蜜,一只蚂蚁在顶点A处,想从盒子的A点爬到盒子的B点,爬行的最短路程是$\sqrt{529}$cm.
如图,无盖的长方体盒子的长为15,宽为10,高为8,在顶点B处(盒子里面)有一滴蜂蜜,一只蚂蚁在顶点A处,想从盒子的A点爬到盒子的B点,爬行的最短路程是$\sqrt{529}$cm.
分析 蚂蚁从A到B有三种爬法,要计算每一种爬法的最短路程必须把长方体盒子展开成平面图形如图,再利用勾股定理计算线段AB的长,进行比较即可.
解答 解:第一种情况:如图1,把我们所看到的前面和右面组成一个平面,
则这个长方形的长和宽分别是25cm和8cm,
则所走的最短线段AB=$\sqrt{2{5}^{2}+{8}^{2}}$=$\sqrt{689}$cm;
第二种情况:如图2,把我们看到的左面与底面组成一个长方形,
则这个长方形的长和宽分别是23cm和10cm,
所以走的最短线段AB=$\sqrt{2{3}^{2}+1{0}^{2}}$=$\sqrt{629}$cm;
第三种情况:如图3,把我们所看到的前面和底面组成一个长方形,
则这个长方形的长和宽分别是15cm和18cm,
所以走的最短线段AB=$\sqrt{1{5}^{2}+1{8}^{2}}$=$\sqrt{549}$cm;
三种情况比较而言,第二种情况最短.
故答案为:$\sqrt{529}$cm.
点评 本题考查平面展开最短路径问题,关键知道蚂蚁爬长方形的对角线长时,路径最短,关键确定长和宽,找到最短路径.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
17.八(1)班组织了一次汉字听写比赛,甲、乙两队各10人,其比赛成绩如下表(10分制):
(1)甲队成绩的中位数是9分,乙队成绩的众数是10分.
(2)计算甲队的平均成绩和方差.
(3)已知乙队成绩的方差是1.4,则成绩较为整齐的是甲队.
| 甲队 | 7 | 8 | 9 | 10 | 10 | 10 | 10 | 9 | 9 | 8 |
| 乙队 | 7 | 7 | 8 | 9 | 10 | 10 | 9 | 10 | 10 | 10 |
(2)计算甲队的平均成绩和方差.
(3)已知乙队成绩的方差是1.4,则成绩较为整齐的是甲队.
1.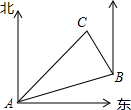 同学甲要从A点出发到距离A点1000米的C地去,他先沿北偏东70°方向到达B地,然后再沿北偏西20°方向走了600米到达目的地C,由此可知AB之间的距离为( )
同学甲要从A点出发到距离A点1000米的C地去,他先沿北偏东70°方向到达B地,然后再沿北偏西20°方向走了600米到达目的地C,由此可知AB之间的距离为( )
 同学甲要从A点出发到距离A点1000米的C地去,他先沿北偏东70°方向到达B地,然后再沿北偏西20°方向走了600米到达目的地C,由此可知AB之间的距离为( )
同学甲要从A点出发到距离A点1000米的C地去,他先沿北偏东70°方向到达B地,然后再沿北偏西20°方向走了600米到达目的地C,由此可知AB之间的距离为( )| A. | 700米 | B. | 700$\sqrt{3}$米 | C. | 800米 | D. | 800$\sqrt{3}$米 |
 如图所示,画出下列几何体的三种视图.
如图所示,画出下列几何体的三种视图. 已知:如图,直线m∥n.Rt△ABC与直线m、n分别相交,且∠1=25°,∠2=80°,求∠A的度数.
已知:如图,直线m∥n.Rt△ABC与直线m、n分别相交,且∠1=25°,∠2=80°,求∠A的度数. 如图,利用一面足够长的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏),设矩形ABCD的宽AD为x米,矩形的长为AB(且AB>AD).
如图,利用一面足够长的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏),设矩形ABCD的宽AD为x米,矩形的长为AB(且AB>AD).