题目内容
6．若$\frac{a}{b}$=$\frac{c}{d}$=$\frac{e}{f}$=$\frac{1}{3}$，则$\frac{a-2c+3e}{b-2d+3f}$=$\frac{1}{3}$．分析 根据$\frac{a}{b}$=$\frac{c}{d}$=$\frac{e}{f}$=$\frac{1}{3}$，得到b=3a，d=3c，f=3e，代入原式即可得到结果．
解答 解：∵$\frac{a}{b}$=$\frac{c}{d}$=$\frac{e}{f}$=$\frac{1}{3}$，
∴b=3a，d=3c，f=3e，
∴$\frac{a-2c+3e}{b-2d+3f}$=$\frac{a-3c+3e}{3a-2（3c）+3（3e）}$=$\frac{a-3c+3e}{3（a-2c+3e）}$=$\frac{1}{3}$．
故答案为：$\frac{1}{3}$．
点评 本题考查了比例的性质，熟记比例的性质是解题的关键．
练习册系列答案
应用题作业本系列答案
相关题目
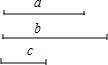已知：线段a、b、c，如图所示，求作：线段x，使2a：b=3c：x．