题目内容
17.已知2x2+3xy-2y2=0(xy≠0),求$\frac{x+y}{x-y}$的值.分析 首先利用因式分解法解方程的方法得出(2x-y)(x+2y)=0,进一步求得x、y之间的关系,进一步代入求得答案即可.
解答 解:∵2x2+3xy-2y2=0(xy≠0),
∴(2x-y)(x+2y)=0,
∴2x-y=0,x+2y=0,
即x=$\frac{1}{2}$y,x=-2y,
当x=$\frac{1}{2}$y时,$\frac{x+y}{x-y}$=-3;
当x=-2y时,$\frac{x+y}{x-y}$=$\frac{1}{3}$.
点评 此题考查因式分解的实际运用,掌握因式分解的方法和代换代入求得答案即可.

练习册系列答案
相关题目
6.若$\frac{a}{b}$=$\frac{c}{d}$=$\frac{e}{f}$=$\frac{1}{3}$,则$\frac{a-2c+3e}{b-2d+3f}$=$\frac{1}{3}$.
6.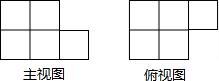 如图,由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数最多是( )
如图,由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数最多是( )
 如图,由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数最多是( )
如图,由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数最多是( )| A. | 7个 | B. | 8个 | C. | 9个 | D. | 10个 |