题目内容
若a、b互为相反数,b、c互为倒数,并且m的立方等于它本身.
(1)试求
+ac值;
(2)若a>1,b<-1,且m<0,S=|2a一3b|-2|b-m|-|b+
|,试求4(2a一S)+2(2a-S)-(2a-S)的值;
(3)若m≠0,当 x为有理数时,|x+m|-|x-m|存在最大值,请求出这个最大值(直接写出答案).
(1)试求
| 2a+2b |
| m+2 |
(2)若a>1,b<-1,且m<0,S=|2a一3b|-2|b-m|-|b+
| 1 |
| 2 |
(3)若m≠0,当 x为有理数时,|x+m|-|x-m|存在最大值,请求出这个最大值(直接写出答案).
考点:代数式求值,相反数,绝对值,倒数
专题:计算题
分析:(1)根据互为相反数的和为零,互为倒数的两个数的积等于1,可得答案;
(2)根据根据不等式的性质,可得2a-3b>0,b+
<0,根据差的绝对值是大数减小数,可化简绝对值得s=2a+
,根据代数式求值,可得答案;
(3)根据m的立方等于它本身m≠0,可得m的值,根据差的绝对值是大数减小数,可得答案.
(2)根据根据不等式的性质,可得2a-3b>0,b+
| 1 |
| 2 |
| 5 |
| 2 |
(3)根据m的立方等于它本身m≠0,可得m的值,根据差的绝对值是大数减小数,可得答案.
解答:解:(1)由题意得a+b=0,bc=1,m=0,±1,
∴ac=-1,
∴原式=0-1=-1;
(2)∵a>1,b<-1,
∴2a-3b>0,b+
<0,
∵m的立方等于它本身,且m<0,
∴m=-1,b-m=b+1<0,
∴s=2a-3b+2b+2+b+
=2a+
,
∴2a-s=-
,
则4(2a-S)+2(2a-S)-(2a-S)=5(2a-S)=-
;
(3)若m≠0,x为有理数时,|x+m|-|x-m|存在最大值为2.
∴ac=-1,
∴原式=0-1=-1;
(2)∵a>1,b<-1,
∴2a-3b>0,b+
| 1 |
| 2 |
∵m的立方等于它本身,且m<0,
∴m=-1,b-m=b+1<0,
∴s=2a-3b+2b+2+b+
| 1 |
| 2 |
| 5 |
| 2 |
∴2a-s=-
| 5 |
| 2 |
则4(2a-S)+2(2a-S)-(2a-S)=5(2a-S)=-
| 25 |
| 2 |
(3)若m≠0,x为有理数时,|x+m|-|x-m|存在最大值为2.
点评:本题考查了代数式求值,(1)利用了相反数、倒数,代数式求值,(2)利用了差的绝对值是大数减小数,(3)利用了差的绝对值是大数减小数.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
若双曲线y=
的图象经过第二、四象限,则k的取值范围是( )
| k |
| x |
| A、k>0 | B、k<0 |
| C、k≠0 | D、不存在 |
已知一次函数y=(m-1)x+m2-1(m为常数),若它的图象过原点,则m( )
| A、m=1 | B、m=±1 |
| C、m=-1 | D、m=0 |
下列说法中,不正确的是( )
| A、经过直线外一点一定存在直线与已知直线平行 |
| B、经过直线上任一点,均不存在与已知直线平行的直线 |
| C、经过直线外一点可以画无数条直线与已知直线平行 |
| D、已知直线外一点有且只有一条直线与已知直线平行 |
 如图,点O是四边形AEBC外接圆的圆心,点O在AB上,点P在BA的延长线上,且∠PEA=∠ADE,CD⊥AB于点H,交⊙O于点D.
如图,点O是四边形AEBC外接圆的圆心,点O在AB上,点P在BA的延长线上,且∠PEA=∠ADE,CD⊥AB于点H,交⊙O于点D.
 如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0
如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0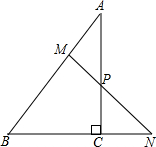 如图,在Rt△ABC中,∠ACB=90°,点P在AC边上,过P点作直线MN交BC延长线于N,交AB于M,且∠APM=∠A.
如图,在Rt△ABC中,∠ACB=90°,点P在AC边上,过P点作直线MN交BC延长线于N,交AB于M,且∠APM=∠A. 如图所示,二次函数y=x2-(a-2)x+a-5的图象交x轴于A和B,交y轴于C,当线段AB最短时,线段OC的长是
如图所示,二次函数y=x2-(a-2)x+a-5的图象交x轴于A和B,交y轴于C,当线段AB最短时,线段OC的长是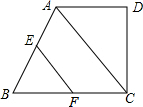 如图,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=CD,点E,F分别是AB,BD的中点,若EF=2,求CD的值.
如图,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=CD,点E,F分别是AB,BD的中点,若EF=2,求CD的值.