题目内容
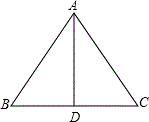 如图,已知等边△ABC的边长为6cm,AD是BC边上的中线.
如图,已知等边△ABC的边长为6cm,AD是BC边上的中线.(1)求AD的长度;
(2)求△ABC的面积.
考点:等边三角形的性质
专题:
分析:(1)证明BD=CD=3,AD⊥BC;运用正切函数求出AD的长.
(2)直接运用三角形的面积公式,求出面积,即可解决问题.
(2)直接运用三角形的面积公式,求出面积,即可解决问题.
解答: 解:(1)∵△ABC是等边三角形,且边长为6,
解:(1)∵△ABC是等边三角形,且边长为6,
∴AB=AC=BC=6,∠B=60°;
∵AD是BC边上的中线,
∴BD=CD=3;AD⊥BC;
∵tan60°=
,
∴AD=3
(cm).
(2)△ABC的面积=
BC•AD
=
×6×3
=9
(cm2).
即△ABC的面积为9
cm2.
 解:(1)∵△ABC是等边三角形,且边长为6,
解:(1)∵△ABC是等边三角形,且边长为6,∴AB=AC=BC=6,∠B=60°;
∵AD是BC边上的中线,
∴BD=CD=3;AD⊥BC;
∵tan60°=
| AD |
| BD |
∴AD=3
| 3 |
(2)△ABC的面积=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 3 |
即△ABC的面积为9
| 3 |
点评:该题主要考查了等边三角形的性质及其应用问题;解题的关键是灵活运用等边三角形的性质,科学求解论证.

练习册系列答案
相关题目
若a,b分别表示一位数,将b放在a的左边,得到的两位数是( )
| A、ba | B、10b+a |
| C、10a+b | D、a+b |
有一人患了流感,经过两轮传染后共有64人患了流感.则每轮传染中平均一个人传染了几个人?( )
| A、10人 | B、6人 | C、7人 | D、8人 |
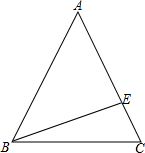 如图,在等腰△ABC中,AB=AC=5,BC=6.
如图,在等腰△ABC中,AB=AC=5,BC=6.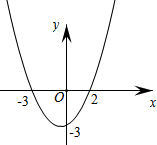 如图抛物线y=ax2+bx+c与x轴交于点(-3,0)、(2,0),与y轴交于点(0,-3),结合图象回答.
如图抛物线y=ax2+bx+c与x轴交于点(-3,0)、(2,0),与y轴交于点(0,-3),结合图象回答.