题目内容
一个正多边形,它的一个外角等于它的相邻的内角,则这个多边形是 边形,共有 条对角线.
考点:多边形内角与外角
专题:
分析:根据多边形的内角和公式及外角的特征计算.可求多边形是四边形,四边形中从一个顶点发出的对角线有1条,因而对角线总的条数即可解得.
解答:解:多边形的外角和是360°,根据题意得:
180°•(n-2)=360°,
解得n=4,
四边形的对角线有:
×4×(4-3)=2条.
答:这个多边形是四边形,共有2条对角线.
故答案为:四,2.
180°•(n-2)=360°,
解得n=4,
四边形的对角线有:
| 1 |
| 2 |
答:这个多边形是四边形,共有2条对角线.
故答案为:四,2.
点评:本题主要考查了多边形内角和公式及外角的特征.求多边形的边数,可以转化为方程的问题来解决.同时考查了n边形的对角线,n边形的对角线有
n(n-3)条.
| 1 |
| 2 |

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
绝对值大于或等于2且小于4的所有整数的积是( )
| A、36 | B、0 | C、-9 | D、-36 |
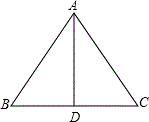 如图,已知等边△ABC的边长为6cm,AD是BC边上的中线.
如图,已知等边△ABC的边长为6cm,AD是BC边上的中线. 如图,△ABC中,∠C=90°,BD=4
如图,△ABC中,∠C=90°,BD=4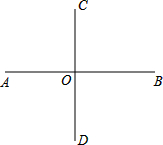 如图,已知AB⊥CD于点O,点E为平面内一点,且∠BOE=60°
如图,已知AB⊥CD于点O,点E为平面内一点,且∠BOE=60° 如图所示,已知AB=DC,AE=DF,CE=BF,求证:AF=DE.
如图所示,已知AB=DC,AE=DF,CE=BF,求证:AF=DE.