题目内容
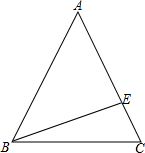 如图,在等腰△ABC中,AB=AC=5,BC=6.
如图,在等腰△ABC中,AB=AC=5,BC=6.(1)求sinB、cosB、tanB的值.
(2)过B作BE⊥AC于点E,假设BC=5m,其他条件不变,求腰上的高BE.
考点:解直角三角形,等腰三角形的性质
专题:
分析:(1)作AD⊥BC,根据等腰三角形底边三线合一性质可求得BD=CD=3,根据勾股定理即可求得AD的长,即可解题;
(2)易判定△ABC为等边三角形,根据BE=BC•sinC即可求得BE的长,即可解题.
(2)易判定△ABC为等边三角形,根据BE=BC•sinC即可求得BE的长,即可解题.
解答:解:(1)作AD⊥BC,
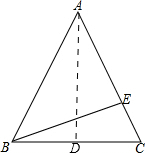
∵AB=AC,AD⊥BC,BC=6,
∴BD=CD=3,
∵AD2=AB2-BD2=16,
∴AD=4,
∴sinB=
=
,cosB
=
,tanB=
=
;
(2)当AB=BC=AC=5时,△ABC为等边三角形,
∴∠C=60°,
∴BE=BC•sinC=
.

∵AB=AC,AD⊥BC,BC=6,
∴BD=CD=3,
∵AD2=AB2-BD2=16,
∴AD=4,
∴sinB=
| AD |
| AB |
| 4 |
| 5 |
| BD |
| AB |
| 3 |
| 5 |
| AD |
| BD |
| 4 |
| 3 |
(2)当AB=BC=AC=5时,△ABC为等边三角形,
∴∠C=60°,
∴BE=BC•sinC=
5
| ||
| 2 |
点评:本题考查了等腰三角形底边三线合一的性质,考查了直角三角形中三角函数运用,考查了直角三角形中勾股定理的运用,考查了特殊角的三角函数值,本题中求得AD的长是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
下列方程是关于x的一元二次方程的是( )
A、x2+
| ||
| B、ax2+bx+c=0 | ||
| C、(x+1)(x-2)=1 | ||
| D、3x2-2xy-5y2=0 |
据统计,截止到今年10月底,我市金融机构存款余额约为1193亿元,用科学记数法应记为( )
| A、1193×109元 |
| B、0.1193×1013元 |
| C、1.193×1011元 |
| D、11.93×1012元 |
今年2月份某市一天的最高气温是12℃,最低气温是-6℃,那么着这一天的最高气温比最低气温高( )
| A、-18℃ | B、18℃ |
| C、6℃ | D、12℃ |
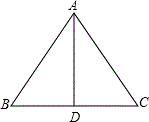 如图,已知等边△ABC的边长为6cm,AD是BC边上的中线.
如图,已知等边△ABC的边长为6cm,AD是BC边上的中线.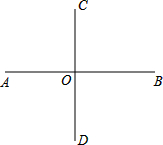 如图,已知AB⊥CD于点O,点E为平面内一点,且∠BOE=60°
如图,已知AB⊥CD于点O,点E为平面内一点,且∠BOE=60° 找出图中所有的同位角、内错角、同旁内角.
找出图中所有的同位角、内错角、同旁内角.