题目内容
2.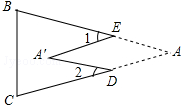 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是2∠A=∠1+∠2.
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是2∠A=∠1+∠2.
分析 连接DE,设∠AED=x,∠ADE=y,根据折叠的性质得∠A′ED=x,∠A′DE=y,根据三角形的内角和定理以及平角的定义,得出∠A与∠1+∠2的关系.
解答  解:连接DE,
解:连接DE,
设∠AED=x,∠ADE=y,
∵△ABC纸片沿DE折叠,
∴∠A′ED=x,∠A′DE=y,
∵∠A+x+y=180,∠1+2x=180,∠2+2y=180,
∴∠1+∠2+2(180-∠A)=2×180,
∴∠1+∠2-2∠A=0,
∴2∠A=∠1+∠2,
故答案为2∠A=∠1+∠2.
点评 本题考查了三角形的内角和定理,以及翻折变换,解题的关键是得出折叠前后不变的角.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
7.下列交换加数位置的变形中,正确的是( )
| A. | 1-4+5-4=1-4+4-5 | |
| B. | 4.5-1.7-2.5+1.8=4.5-2.5+1.8-1.7 | |
| C. | 1-2+3-4=2-1+4-3 | |
| D. | -$\frac{1}{3}$+$\frac{3}{4}$-$\frac{1}{6}$-$\frac{1}{4}$=$\frac{1}{4}$+$\frac{3}{4}$-$\frac{1}{3}$-$\frac{1}{6}$ |
14.已知y=ax2(a≠0)的图象不经过第四象限,图象上有A(-1,y1),B(-$\sqrt{2}$,y2),C(2,y3)三点,则y1、y2、y3的大小关系为( )
| A. | y1<y2<y3 | B. | y1>y2>y3 | C. | y2>y1>y3 | D. | y3>y1>y2 |
 如图,从一张半圆形的铁片上剪下了一个小的半圆形铁片,为了计算剩余部分的面积,小亮在图中作出一条小圆的切线,并使它平行于大圆的直径.设这条切线交大圆于点A,B,量得AB的长是a,便可求出剩余部分的面积.请你说出小亮是如何算出来的.
如图,从一张半圆形的铁片上剪下了一个小的半圆形铁片,为了计算剩余部分的面积,小亮在图中作出一条小圆的切线,并使它平行于大圆的直径.设这条切线交大圆于点A,B,量得AB的长是a,便可求出剩余部分的面积.请你说出小亮是如何算出来的.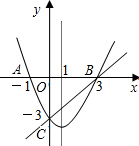 如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),一次函数的图象与抛物线交于B、C两点.
如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),一次函数的图象与抛物线交于B、C两点.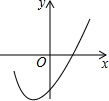 如图二次函数y=ax2+bx+c的部分图象及顶点坐标(-1,-3.2),由图象可知关于x的方程ax2+bx+c=0的两根x1=1.3,x2=-3.3.
如图二次函数y=ax2+bx+c的部分图象及顶点坐标(-1,-3.2),由图象可知关于x的方程ax2+bx+c=0的两根x1=1.3,x2=-3.3.