题目内容
14.已知y=ax2(a≠0)的图象不经过第四象限,图象上有A(-1,y1),B(-$\sqrt{2}$,y2),C(2,y3)三点,则y1、y2、y3的大小关系为( )| A. | y1<y2<y3 | B. | y1>y2>y3 | C. | y2>y1>y3 | D. | y3>y1>y2 |
分析 关键题意可知a>0.对称轴x=0,则A、B、C的横坐标离对称轴越近,则纵坐标越小,由此判断y1、y2、y3的大小.
解答 解:∵y=ax2(a≠0)的图象不经过第四象限,
∴a>0,
在二次函数y=ax2(a≠0),对称轴y轴,
图象上有A(-1,y1),B(-$\sqrt{2}$,y2),C(2,y3)三点,
|-1|<|-$\sqrt{2}$|<|2|,
则y1、y2、y3的大小关系为y1<y2<y3.
故选A.
点评 本题考查了二次函数图象上点的坐标特征,由点的横坐标到对称轴的距离判断点的纵坐标的大小.

练习册系列答案
相关题目
4.计算:-4×[-(-2)]的结果是( )
| A. | -8 | B. | 8 | C. | 2 | D. | -2 |
5. 已知二次函数y=ax2+bx+c的图象如图所示,则不正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则不正确的是( )
 已知二次函数y=ax2+bx+c的图象如图所示,则不正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则不正确的是( )| A. | C>0 | B. | a+b+c<0 | C. | a<0 | D. | b>0 |
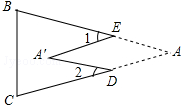 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是2∠A=∠1+∠2.
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是2∠A=∠1+∠2.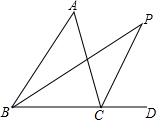 如图,△ABC的内角平分线BP和外角平分线CP交于点P,∠A=52°,则∠P=26°.
如图,△ABC的内角平分线BP和外角平分线CP交于点P,∠A=52°,则∠P=26°.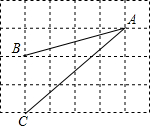 如图,在6×5的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则sin∠BAC的值为$\frac{8\sqrt{17}}{85}$.
如图,在6×5的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则sin∠BAC的值为$\frac{8\sqrt{17}}{85}$.