题目内容
13. 如图,从一张半圆形的铁片上剪下了一个小的半圆形铁片,为了计算剩余部分的面积,小亮在图中作出一条小圆的切线,并使它平行于大圆的直径.设这条切线交大圆于点A,B,量得AB的长是a,便可求出剩余部分的面积.请你说出小亮是如何算出来的.
如图,从一张半圆形的铁片上剪下了一个小的半圆形铁片,为了计算剩余部分的面积,小亮在图中作出一条小圆的切线,并使它平行于大圆的直径.设这条切线交大圆于点A,B,量得AB的长是a,便可求出剩余部分的面积.请你说出小亮是如何算出来的.
分析 将小圆平移到如图所示的位置,则阴影部分的面积=两个半圆的面积之差.
解答 解:剩余部分的面积=$\frac{1}{2}π{{r}_{大}}^{2}$-$\frac{1}{2}π{r}_{小}^{2}$.
将小圆平移到如图所示的位置.
∵AB是小圆的切线,
∴OD⊥AB.
∴DB=$\frac{1}{2}AB$=$\frac{1}{2}a$.
在Rt△DBO中,OB2-OD2=DB2=$\frac{1}{4}{a}^{2}$.
∴剩余部分的面积=$\frac{1}{2}π•\frac{1}{4}{a}^{2}$=$\frac{π{a}^{2}}{8}$.
点评 本题主要考查的是切线的性质、垂径定理、平移的性质的应用,经过平移将两个圆的圆心重合是解题的关键.

练习册系列答案
相关题目
4.计算:-4×[-(-2)]的结果是( )
| A. | -8 | B. | 8 | C. | 2 | D. | -2 |
5. 已知二次函数y=ax2+bx+c的图象如图所示,则不正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则不正确的是( )
 已知二次函数y=ax2+bx+c的图象如图所示,则不正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则不正确的是( )| A. | C>0 | B. | a+b+c<0 | C. | a<0 | D. | b>0 |

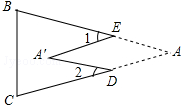 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是2∠A=∠1+∠2.
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是2∠A=∠1+∠2.