题目内容
19．计算：（1）$\frac{\sqrt{20}-\sqrt{5}}{\sqrt{5}}$
（2）$\sqrt{3}×（\sqrt{6}-2\sqrt{3}）$$+3\sqrt{2}$．
分析 （1）根据二次根式的除法法则进行计算即可；
（2）先根据二次根式的乘法法则进行计算，再合并即可．
解答 解：（1）$\frac{\sqrt{20}-\sqrt{5}}{\sqrt{5}}$
=$\sqrt{4}$-1
=2-1
=1；
（2）$\sqrt{3}×（\sqrt{6}-2\sqrt{3}）$$+3\sqrt{2}$
=3$\sqrt{2}$-6+3$\sqrt{2}$
=6$\sqrt{2}$-6．
点评 本题考查了二次根式的混合运算的应用，能熟记二次根式的运算法则是解此题的关键．
练习册系列答案
相关题目
9．若反比例函数y=-$\frac{k}{|x|}$（k≠0）的图象经过点（-5，-3），则反比例函数的图象分布在（ ）
| A． | 第一、三象限 | B． | 第二、四象限 | C． | 第一、二象限 | D． | 第三、四象限 |
10．给出四个数0，0.5，$\sqrt{2}$，3，其中为无理数的是（ ）
| A． | 0 | B． | 0.5 | C． | 3 | D． | $\sqrt{2}$ |
14．函数y=（m-4）x+2m-3的图象经过一、二、四象限，那么m的取值范围是（ ）
| A． | m＜4 | B． | 1.5＜m＜4 | C． | -1.5＜m＜4 | D． | m＞4 |
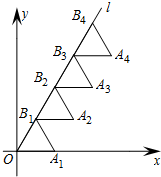如图放置的△OB1A1，△B1B2A2，△B2B3A3，…，都是边长为2的等边三角形，边OA1在x轴上，且点O，B1，B2，B3，…，都在同一直线上，则A2015的坐标是（2016，2014$\sqrt{3}$）．
11．下列算式正确的是（ ）
| A． | $\sqrt{2}•\sqrt{3}=\sqrt{6}$ | B． | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | C． | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ | D． | $\sqrt{8}÷\sqrt{2}=4$ |