题目内容
4.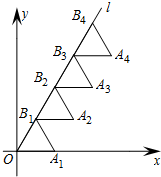 如图放置的△OB1A1,△B1B2A2,△B2B3A3,…,都是边长为2的等边三角形,边OA1在x轴上,且点O,B1,B2,B3,…,都在同一直线上,则A2015的坐标是(2016,2014$\sqrt{3}$).
如图放置的△OB1A1,△B1B2A2,△B2B3A3,…,都是边长为2的等边三角形,边OA1在x轴上,且点O,B1,B2,B3,…,都在同一直线上,则A2015的坐标是(2016,2014$\sqrt{3}$).
分析 过B1向x轴作垂线B1C,根据等边三角形性质及三角函数的应用求得点A1、B1坐标,继而可得点A2坐标,同理得出点A3、A4坐标,根据以上规律即可得.
解答 解:过B1向x轴作垂线B1C,垂足为C,
由题意可得:OB1=OA1=2,∠A1OB1=60°,
∴点A1坐标为(2,0),OC=$\frac{1}{2}$OB1=1,CB1=OB1sin60°=$\sqrt{3}$,
∴B1的坐标为:(1,$\sqrt{3}$),
∵B1A2∥x轴,B1A2=2,
∴点A2坐标为(3,$\sqrt{3}$),
同理可得点A3坐标为(4,2$\sqrt{3}$),
点A4坐标为(5,3$\sqrt{3}$),
∴点A2015坐标为(2016,2014$\sqrt{3}$),
故答案为:(2016,2014$\sqrt{3}$).
点评 此题主要考查了一次函数图象上点的坐标特征以及数字变化类,得出A点横纵坐标变化规律是解题关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
14.以下列各组线段长为边能组成三角形的是( )
| A. | 1cm 2cm 4cm | B. | 8cm 6cm 4cm | C. | 12cm 5cm 6cm | D. | 2cm 3cm 6cm |
9.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
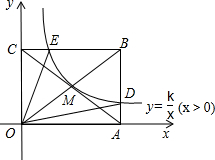 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB,BC交于点D,E,若四边形ODBE的面积为6,则△OAD的面积为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB,BC交于点D,E,若四边形ODBE的面积为6,则△OAD的面积为( )