题目内容
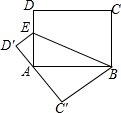 如图,已知点E是长方形ABCD中AD边上一点,将四边形BCDE沿直线BE折叠,折叠后点C的对应点为C′,点D的对应点为D′,若点A在C′D′上,且AB=5,BC=4,则AE=
如图,已知点E是长方形ABCD中AD边上一点,将四边形BCDE沿直线BE折叠,折叠后点C的对应点为C′,点D的对应点为D′,若点A在C′D′上,且AB=5,BC=4,则AE=考点:翻折变换(折叠问题)
专题:
分析:如图,求出AC′=3,AD′=2;证明ED=ED′(设为λ),得到AE=4-λ;运用勾股定理列出关于λ的方程,求出λ即可解决问题.
解答: 解:如图,∵四边形ABCD为矩形,
解:如图,∵四边形ABCD为矩形,
∴∠D=∠C=∠DAB=90°;
AB=DC=5,AD=BC=4;
根据翻折变换的性质可知:
∠D′=∠D=90°,∠C′=∠C=90°;
BC′=BC=4,D′C′=DC=5;
由勾股定理得:
AC′2=AB2-BC′2,
∴AC′=3,AD′=5-3=2;
由题意得:ED=ED′(设为λ),则AE=4-λ;
由勾股定理得:(4-λ)2=22+λ2,
解得:λ=
,AE=
.
故答案为
.
 解:如图,∵四边形ABCD为矩形,
解:如图,∵四边形ABCD为矩形,∴∠D=∠C=∠DAB=90°;
AB=DC=5,AD=BC=4;
根据翻折变换的性质可知:
∠D′=∠D=90°,∠C′=∠C=90°;
BC′=BC=4,D′C′=DC=5;
由勾股定理得:
AC′2=AB2-BC′2,
∴AC′=3,AD′=5-3=2;
由题意得:ED=ED′(设为λ),则AE=4-λ;
由勾股定理得:(4-λ)2=22+λ2,
解得:λ=
| 5 |
| 2 |
| 3 |
| 2 |
故答案为
| 5 |
| 2 |
点评:该题主要考查了翻折变换、矩形的性质、勾股定理及其应用问题;牢固掌握矩形的性质、勾股定理等是解题的关键.

练习册系列答案
相关题目
 如图,△ABC内接于⊙O,AB过点O,若∠BAC=30°,则∠B的度数为( )
如图,△ABC内接于⊙O,AB过点O,若∠BAC=30°,则∠B的度数为( )| A、55° | B、60° |
| C、65° | D、70° |
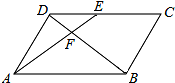 如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:AB=( )
如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:AB=( )| A、2:5 | B、2:3 |
| C、3:5 | D、3:2 |
 如图,已知⊙O的半径为5cm,弦AB=8cm,则圆心O到弦AB的距离是( )
如图,已知⊙O的半径为5cm,弦AB=8cm,则圆心O到弦AB的距离是( )| A、1cm | B、2cm |
| C、3cm | D、4cm |
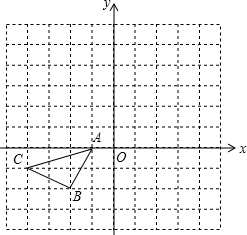 在如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
在如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: 如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数. 在△ABC中,AB=9,AC=5,AD是∠BAC的平分线交BC于点D(如图),△ABD沿直线AD翻折后,点B落到点B1处,如果∠B1DC=
在△ABC中,AB=9,AC=5,AD是∠BAC的平分线交BC于点D(如图),△ABD沿直线AD翻折后,点B落到点B1处,如果∠B1DC=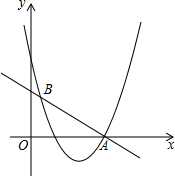 如图,直线y=-
如图,直线y=-