题目内容
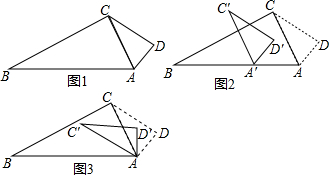
12．下列图形中，轴对称图形的个数是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形进行分析即可．
解答 解：第一个，是轴对称图形，符合题意；
第二个，不是轴对称图形，不合题意；
第三个，是轴对称图形，符合题意；
第四个，是轴对称图形，符合题意．
故选：C．
点评 此题主要考查了轴对称图形，关键是掌握轴对称图形的定义．
练习册系列答案
相关题目
20．某科技公司研发出一款多型号的智能手表，一家代理商出售该公司的A型智能手表，去年销售总额为80000元，今年A型智能手表的售价每只比去年降了600元，若售出的数量与去年相同，销售总额将比去年减少25%．
（1）请问今年A型智能手表每只售价多少元？
（2）今年这家代理商准备新进一批A型智能手表和B型智能手表共100只，它们的进货价与销售价格如右表，若B型智能手表进货量不超过A型智能手表数量的3倍，所进智能手表可全部售完，请你设计出进货方案，使这批智能手表获利最多，并求出最大利润是多少元？
| A型智能手表 | B型智能手表 | |
| 进价 | 1300元/只 | 1500元/只 |
| 售价 | 今年的售价 | 2300元/只 |
（2）今年这家代理商准备新进一批A型智能手表和B型智能手表共100只，它们的进货价与销售价格如右表，若B型智能手表进货量不超过A型智能手表数量的3倍，所进智能手表可全部售完，请你设计出进货方案，使这批智能手表获利最多，并求出最大利润是多少元？
7．据襄阳新闻报道2016年3月至2016年10月，襄阳闸口二路“大虾一条街”共销售大虾6000余吨.2017年潜江养虾专业户张小花抓住商机，将自己养殖的大虾销往襄阳．计算了养殖成本以及运费等诸多因素，他发现大虾的成本价为20元/公斤．经过市场调查，一周的销售量y公斤与销售单价x（x≥30）元/公斤的关系如下表：
（1）直接写出y与x的函数关系式；
（2）若张小花一周的销售利润为W元，请求出W与x的函数关系式，并确定当销售单价在什么范围内变化时，一周的销售利润随着销售单价的增大而增大？
（3）随着赚的钱越来越多，张小花决定回馈社会将一周的销售利润全部捐给襄阳市福利院．若一周张小花的总成本不超过4000元，请求出张小花最大捐款数额是多少元？
| 销售单价x元/公斤 | … | 30 | 35 | 40 | 45 | … |
| 销售量y公斤 | … | 500 | 450 | 400 | 350 | … |
（2）若张小花一周的销售利润为W元，请求出W与x的函数关系式，并确定当销售单价在什么范围内变化时，一周的销售利润随着销售单价的增大而增大？
（3）随着赚的钱越来越多，张小花决定回馈社会将一周的销售利润全部捐给襄阳市福利院．若一周张小花的总成本不超过4000元，请求出张小花最大捐款数额是多少元？
17．
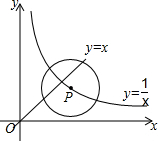如图，点P是函数y=$\frac{1}{x}$（x＞0）的图象上的一点，⊙P的半径为$\sqrt{2}$，当⊙P与直线y=x有公共点时，点P的横坐标x的取值范围是（ ）
如图，点P是函数y=$\frac{1}{x}$（x＞0）的图象上的一点，⊙P的半径为$\sqrt{2}$，当⊙P与直线y=x有公共点时，点P的横坐标x的取值范围是（ ）| A． | 1≤x≤$\sqrt{2}$ | B． | $\sqrt{2}-1≤x≤\sqrt{2}$ | C． | $\sqrt{2}-1≤x≤1$ | D． | $\sqrt{2}-1≤x≤\sqrt{2}+1$ |
4．
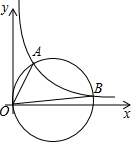如图，点A（1，2）在反比例函数y=$\frac{k}{x}$（x＞0）上，B为反比例函数图象上一点，不与A重合，当以OB为直径的圆经过A点，点B的坐标为（ ）
如图，点A（1，2）在反比例函数y=$\frac{k}{x}$（x＞0）上，B为反比例函数图象上一点，不与A重合，当以OB为直径的圆经过A点，点B的坐标为（ ）| A． | （2，1） | B． | （3，$\frac{2}{3}$） | C． | （4，0.5） | D． | （5，0.4） |
1．
如图所示，直线l1∥l2，三角尺的一个顶点在l2上，若∠1=70°，则∠2=（ ）
如图所示，直线l1∥l2，三角尺的一个顶点在l2上，若∠1=70°，则∠2=（ ）| A． | 70° | B． | 60° | C． | 40° | D． | 30° |
