题目内容
2.小明拿两个大小不等直角三角板作拼图,如图①小三角板的斜边与大三角板直角边正好重合,已知:AD=1,∠B=∠ACD=30°.(1)AB的长4;四边形ABCD的面积=$\frac{5\sqrt{3}}{2}$(直接填空);
(2)如图2,若小明将小三角板ACD沿着射线AB方向平移,设平移的距离为m(平移距离指点A沿AB方向锁经过的线段长度),当点D平移到线段大三角板ABC的边上时,求出相应的m的值;
(3)如图3,小明将小三角板ACD绕点A顺时针旋转一个角α(0°<α<180°),记旋转中的△ACD为△AC′D′,在旋转过程中,设C′D′所在的直线与直线BC交于点P,与直线AB交于点Q,是否存在这样的P、Q两点,使△BPQ为等腰三角形?若存在,请直接求出此时D′Q的长;若不存在,请说明理由
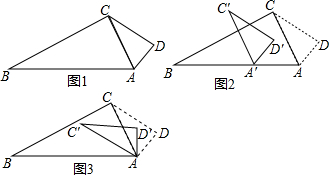
分析 (1)根据30度的直角三角形的性质,求出AC、CD、AB、BC即可解决问题;
(2)如图2中,作DE∥AB交BC于E,交AC于F.求出DF、DE即可解决问题;
(3)分三种情形求解①如图3中,当BP=BQ时,②如图4中,当BQ=PQ时,③如图5中,当BP=BQ时,分别求解即可;
解答 解:(1)如图1中,
在Rt△ACD中,∵AD=1,∠ACD=30°,
∴AC=2CD=2,CD=$\sqrt{3}$AD=$\sqrt{3}$,
在Rt△ACB中,∵∠B=30°,AC=2,
∴AB=2AC=4,BC=$\sqrt{3}$AC=2$\sqrt{3}$,
∴四边形ABCD的面积=S△ACD+S△ABC=$\frac{1}{2}$$•1•\sqrt{3}$+$\frac{1}{2}$•2•2$\sqrt{3}$=$\frac{5\sqrt{3}}{2}$.
故答案为4,$\frac{5\sqrt{3}}{2}$.
(2)如图2中,作DE∥AB交BC于E,交AC于F.
∴∠DFA=∠BAC=60°=∠DAF,
∴△ADF是等边三角形,
∴AF=AD=DF=CF=1,∵FE∥AB,
∴CE=EB,
∴EF=$\frac{1}{2}$AB=2,
∴当点D平移到线段大三角板ABC的边上时,相应的m的值为1或3.
(3)①如图3中,当BP=BQ时,在AD′上取一点E使得AE=EQ.
∵∠PBQ=30°,
∴∠AQD′=75°,∵∠AD′Q=90°,
∴∠EAQ=∠EQA=15°
∴∠QED′=30°,设D′Q=x,则AE=EQ=2x,ED′=$\sqrt{3}$x,
∴2x+$\sqrt{3}$x=1,
∴x=2-$\sqrt{3}$,
∴D′Q=2-$\sqrt{3}$.
②如图4中,当BQ=PQ时,易知∠AQD′=60°,D′Q=AD•tan30°=$\frac{\sqrt{3}}{3}$.
③如图5中,当BP=BQ时,易知∠AQC′=∠C′AQ=15°,∴AC′=C′Q,∴D′Q=D′C+C′Q′=$\sqrt{3}$+2.
综上所述,当△PBQ是等腰三角形时,D′Q的值为2-$\sqrt{3}$或$\frac{\sqrt{3}}{3}$或$\sqrt{3}$+2.
点评 本题考查四边形综合题、旋转变换、30度的直角三角形的性质、等腰三角形的判定和性质、三角形的中位线定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 50° | B. | 60° | C. | 45° | D. | 120° |
| A. |  | B. |  | C. |  | D. |  |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 85%a10%×90 | B. | 90×85%×10%=a | C. | 85%(90-a)=10% | D. | (1+10%)a=90×85% |
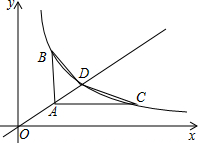 直线y=$\frac{2}{3}x$与双曲线y=$\frac{6}{x}$(x>0)相交于点D.
直线y=$\frac{2}{3}x$与双曲线y=$\frac{6}{x}$(x>0)相交于点D. 如图是由四个相同的小立方体搭成的几何体,则它的左视图是( )
如图是由四个相同的小立方体搭成的几何体,则它的左视图是( )


