题目内容
4.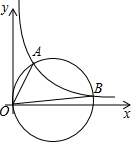 如图,点A(1,2)在反比例函数y=$\frac{k}{x}$(x>0)上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为( )
如图,点A(1,2)在反比例函数y=$\frac{k}{x}$(x>0)上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为( )| A. | (2,1) | B. | (3,$\frac{2}{3}$) | C. | (4,0.5) | D. | (5,0.4) |
分析 求得解析式y=$\frac{2}{x}$,设B(m,$\frac{2}{m}$),如图,证△AOC∽△BAD得$\frac{AC}{BD}$=$\frac{OC}{AD}$,即$\frac{1}{2-\frac{2}{m}}$=$\frac{2}{m-1}$,求得m的值即可.
解答 解:将点A(1,2)代入y=$\frac{k}{x}$,得:k=2,
则反比例函数解析式为y=$\frac{2}{x}$,
设点B(m,$\frac{2}{m}$),
如图,连接AB,过点A作x轴的平行线,交y轴于点C,过点B作y轴的平行线,交直线AC于点D,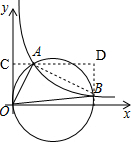
则∠OCA=∠D=90°,
∴∠AOC+∠OAC=90°,
∵OB为圆的直径,
∴∠OAB=90°,
∴∠OAC+∠BAD=90°,
∴∠AOC=∠BAD,
则△AOC∽△BAD,
∴$\frac{AC}{BD}$=$\frac{OC}{AD}$,即$\frac{1}{2-\frac{2}{m}}$=$\frac{2}{m-1}$,
解得:m=1(舍)或m=4,
则点B(4,0.5),
故选:C.
点评 本题主要考查反比例函数图象上点的坐标特征及相似三角形的判定与性质、圆周角定理,根据相似三角形的判定与性质建立方程是解题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
15.若0<a<b,$\sqrt{\frac{a}{b}}$+$\sqrt{\frac{b}{a}}$=$\sqrt{6}$,则$\frac{a-b}{a+b}$的值是( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | -$\sqrt{3}$ | C. | -$\frac{\sqrt{6}}{2}$ | D. | -$\frac{\sqrt{3}}{3}$ |
12.下列图形中,轴对称图形的个数是( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.若∠A与∠B互为余角,则∠A+∠B=( )
| A. | 180° | B. | 120° | C. | 90° | D. | 60° |
13.一个正多边形的内角和是外角和的2倍,则这个正多边形的每个外角为( )
| A. | 50° | B. | 60° | C. | 45° | D. | 120° |
14.一次函数y=3x+2的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |