题目内容
15.已知点P(m,3),Q(-5,n),根据以下要求确定m,n的值或范围.(1)点Q在x轴上且点P在y轴上;
(2)PQ∥x轴;
(3)点P与点Q都在第二、四象限的角平分线上.
分析 (1)根据x轴上的点纵坐标为0,y轴上的点横坐标为0即可解决.
(2)根据平行于x轴的两点纵坐标相同,横坐标不能相同即可解决.
(3)根据二、四象限的角平分线上点的特征横坐标与纵坐标互为相反数即可解决.
解答 解;(1)∵点Q在x轴上且点P在y轴上,
∴m=0,n=0,
(2)∵PQ∥x轴,
∴P、Q两点的纵坐标相同,横坐标不能相同,
即n=3,m≠-5
(3)∵点P与点Q都在第二、四象限的角平分线上,
∴P、Q两点的横坐标与纵坐标互为相反数,
∴m=-3,n=5.
点评 本题考查坐标与图形的性质,记住坐标轴上的点的特征、两个象限的角平分线上的点的特征是解决问题的关键,属于中考常考题型.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5.若关于x的一元二次方程kx2-4x+2=0有实数根,则k的非负整数值为( )
| A. | 1 | B. | 0,1 | C. | 1,2 | D. | 0,1,2 |
6.下列所给函数中,y随x的增大而减小的是( )
| A. | y=-x-1 | B. | y=2x2(x≥0) | C. | $y=-\frac{2}{x}$ | D. | y=x+1 |
3.2015年十一国庆长假提前到9月29日,黄金周期间外出旅游更为火爆,若旅游区的门票为60元/张,某旅游区的开放时间为每天10小时,并每小时对进入旅游区的游客人数进行一次统计,下表是9月30日对进入旅游区人数的7次抽样统计数据:
那么从9月29日至10月5日旅游区门票收入是多少?( )
| 记数的次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 |
| 每小时进入旅游区的人数 | 318 | 310 | 310 | 286 | 280 | 312 | 284 |
| A. | 900000元 | B. | 1260000元 | C. | 191600元 | D. | 162000元 |
10.三位同学参加数理化竞赛,每人限报一项,甲报数学、乙报物理、丙报化学的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{27}$ |
7.下列结论中正确的是( )
| A. | a3+a2=a5 | B. | a3•a2=a6 | C. | a3÷a2=a | D. | (a3)2=a5 |
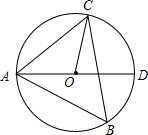 如图,△ABC内接于⊙O,AD是直径,sinB=$\frac{5}{34}$$\sqrt{34}$.
如图,△ABC内接于⊙O,AD是直径,sinB=$\frac{5}{34}$$\sqrt{34}$.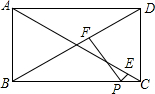 如图,矩形ABCD中,点P在BC边上,PE⊥AC,PF⊥BD,AB=6,BC=8,运用上述结论,求PE+PF的值.
如图,矩形ABCD中,点P在BC边上,PE⊥AC,PF⊥BD,AB=6,BC=8,运用上述结论,求PE+PF的值.