��Ŀ����
19����֪������y=ax2+bx-4��x�ύ��A��B���㣬����B�ڵ�A����ࣩ��A��B���������ֱ�Ϊ��-2��0������8��0������y�ύ�ڵ�C������BC����BCΪһ�ߣ���OΪ�Գ�����������BDEC����P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���L���������ڵ�Q����BD�ڵ�M��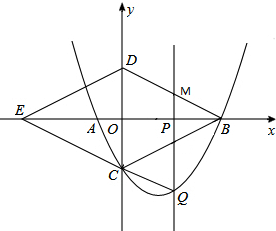
��1���������ߵĽ���ʽ��
��2������P���߶�OB���˶�ʱ����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı��Σ�
��3���ڣ�2���Ľ����£��������������Ƿ���ڵ�N����ͬ�ڵ�Q����ʹ������BCN���������������BCQ������������ڣ��������N�����ꣻ�������ڣ���˵�����ɣ�
���� ��1�����ݴ���ϵ����������ã�
��2�������εĶԳ��Կ�֪����D�����꣬���ݴ���ϵ��������ֱ��BD�Ľ���ʽ������ƽ���ı��ε����ʿɵù���m�ķ��̣����m��ֵ���ٸ���ƽ���ı��ε��ж��ɵ��ı���CQMD����״��
��3��Ҫʹ������BCN���������������BCQ����������ж��ı���CQBN��ƽ���ı��Σ���ô�ʱ��N�����꼴�ɣ�
��� �⣺��1����������y=ax2+bx-4��x�ύ��A��-2��0����B��8��0�����㣬
��$\left\{\begin{array}{l}{0=4a-2b-4}\\{0=64a+8b-4}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=\frac{1}{4}}\\{b=-\frac{3}{2}}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4��
��2����C��0��-4��
�������εĶԳ��Կ�֪����D������Ϊ��0��4����
��ֱ��BD�Ľ���ʽΪy=kx+b����$\left\{\begin{array}{l}{b=4}\\{8k+b=0}\end{array}\right.$��
���k=-$\frac{1}{2}$��b=4��
��ֱ��BD�Ľ���ʽΪy=-$\frac{1}{2}$x+4��
��l��x�ᣬ
���M��������m��-$\frac{1}{2}$m+4������Q��������m��$\frac{1}{4}$m2-$\frac{3}{2}$m-4����
��ͼ����MQ=DCʱ���ı���CQMD��ƽ���ı��Σ�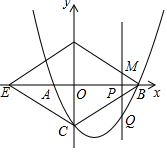
�ࣨ-$\frac{1}{2}$m+4��-�� $\frac{1}{4}$m2-$\frac{3}{2}$m-4��=4-��-4����
����ã�m2-4m=0��
���m1=0������������ȥ����m2=4��
�൱m=4ʱ���ı���CQMD��ƽ���ı��Σ�
��3��Ҫʹ������BCN���������������BCQ�������
N�㵽BC�ľ�����Q��BC�ľ�����ȣ����Թ�M��Q���б��Ϊ$\frac{1}{2}$�� ֱ���������ߵĽ��㼴Ϊ����
M��4��2����Q��4��-6��
��ֱ��l��y=$\frac{1}{2}$x+b
�ٵ�ֱ��l��Q��ʱ��
����l��y=$\frac{1}{2}$x-8
���������߷��̣�$\frac{1}{4}$x2-$\frac{3}{2}$x-4=$\frac{1}{2}$x-8�����x1=x2=4����Q�غϣ���ȥ��
�ڵ�ֱ�߹�M��ʱ������
l��y=$\frac{1}{2}x$��
���������߷��̣�$\frac{1}{4}$x2-$\frac{3}{2}$x-4=$\frac{1}{2}$x�����x1=4+$4\sqrt{2}$��x2=4-$4\sqrt{2}$������ֱ�߷��̣����
N1��4+4$\sqrt{2}$��2+2$\sqrt{2}$����N2��4-4$\sqrt{2}$��2-2$\sqrt{2}$����
�ʷ���������N������ΪN1��4+4$\sqrt{2}$��2+2$\sqrt{2}$����N2��4-4$\sqrt{2}$��2-2$\sqrt{2}$����
���� ���⿼���˶��κ����ۺ��ԣ��漰��֪ʶ���У��������ϵ���ص㣬���εĶԳ��ԣ�����ϵ������ֱ�ߵĽ���ʽ��ƽ���ı��ε��ж������ʣ�����˼��ͷ���˼������ã��ۺ��Խ�ǿ����һ�����Ѷȣ�

 �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д� ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д� �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�| A�� | һ����������ȵ�ʵ���� | B�� | һ����ʵ���� | ||
| C�� | һ������������ȵ�ʵ���� | D�� | һ��û��ʵ���� |
| A�� | $\sqrt{��-2��^{2}}$=-2 | B�� | ��-$\sqrt{3}$��2=9 | C�� | $\root{3}{-9}$=-3 | D�� | ��$\sqrt{9}$=��3 |
 ���в���ʽ��Ľ⼯���������ϱ�ʾΪ��ͼ��ʾ���ǣ�������
���в���ʽ��Ľ⼯���������ϱ�ʾΪ��ͼ��ʾ���ǣ�������| A�� | $\left\{\begin{array}{l}{x-1��0}\\{x+2��0}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x+1��0}\\{x-2��0}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x+1��0}\\{x-2��0}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x-1��0}\\{x+2��0}\end{array}\right.$ |
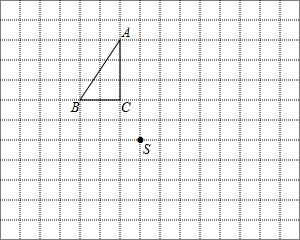 ��ABC�͵�S��������������ĸ���ϣ�ÿ��С�����εı߳�Ϊ1��
��ABC�͵�S��������������ĸ���ϣ�ÿ��С�����εı߳�Ϊ1��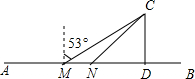 ������ͭ��������Ϊ����������Σ������ˡ���������������A���С���Ķ��̬ʪ�غɻ���������B���С�ɳ��õ������Ϊ����ʵ��һ�ٴ룬�������ƻ���A��B�����ξ���֮����һ����·AB����֪��·AB��һ���С��ļ�����������C���ڹ�·AB�ϵ�M����þ���C��M�ı�ƫ��53�㷽���ϣ���M����300����N������þ���C��N�Ķ��������ϣ��Ҿ���C��Χ800��Χ��Ϊ���ļ���������
������ͭ��������Ϊ����������Σ������ˡ���������������A���С���Ķ��̬ʪ�غɻ���������B���С�ɳ��õ������Ϊ����ʵ��һ�ٴ룬�������ƻ���A��B�����ξ���֮����һ����·AB����֪��·AB��һ���С��ļ�����������C���ڹ�·AB�ϵ�M����þ���C��M�ı�ƫ��53�㷽���ϣ���M����300����N������þ���C��N�Ķ��������ϣ��Ҿ���C��Χ800��Χ��Ϊ���ļ���������