题目内容
2.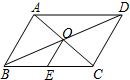 如图,在?ABCD中,对角线AC、BD交于点O,E是BC边上的中点,若OE=2,AC+BD=12,则△OAB的周长为10.
如图,在?ABCD中,对角线AC、BD交于点O,E是BC边上的中点,若OE=2,AC+BD=12,则△OAB的周长为10.
分析 由平行四边形的性质求出OA+OB=6,证明OE是△ABC的中位线,由三角形中位线定理得出AB=2OE=4,即可得出△OAB的周长.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,
∴OA+OB=$\frac{1}{2}$(AC+BD)=6,
∵E是BC边上的中点,
∴OE是△ABC的中位线,
∴AB=2OE=4,
∴△OAB的周长=OA+OB+AB=6+4=10,
故答案为:10.
点评 本题考查了平行四边形的性质、三角形的中位线定理;熟练掌握平行四边形的性质,由平行四边形的性质求出OA+OB是解决问题的关键.

练习册系列答案
相关题目
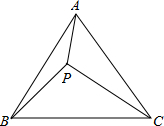 已知,如图,P为等边三角形ABC内一点,PA=3,PB=4,PC=5,求△ABC的面积.
已知,如图,P为等边三角形ABC内一点,PA=3,PB=4,PC=5,求△ABC的面积.