题目内容
14.函数$y=\frac{2x}{{\sqrt{x+1}}}$的自变量x的取值范围是x>-1.分析 根据被开方数大于等于0,分母不等于0列式计算即可得解.
解答 解:由题意得,x+1>0,
解得x>-1.
故答案为:x>-1.
点评 本题考查了函数自变量的范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
相关题目
4.在下列各式①$\frac{1}{2}$(1-x);②$\frac{2x}{π-3}$;③$\frac{{x}^{2}-{y}^{2}}{2}$;④$\frac{3}{x+y}$;⑤$\frac{5{y}^{2}}{x}$中,是分式有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
19.下列各组数据分别是三角形的三边长,其中能构成直角三角形的是( )
| A. | 2cm、4cm、5cm | B. | 1cm、1cm、$\sqrt{2}$cm | C. | 1cm、2cm、2cm | D. | $\sqrt{3}$cm、2cm、$\sqrt{5}$cm |
3.点P位于第一象限,距y轴3个单位长度,距离x轴4个单位长度,则点P坐标是( )
| A. | (-3,4) | B. | (3,4) | C. | (-4,3) | D. | (4,3) |
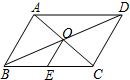 如图,在?ABCD中,对角线AC、BD交于点O,E是BC边上的中点,若OE=2,AC+BD=12,则△OAB的周长为10.
如图,在?ABCD中,对角线AC、BD交于点O,E是BC边上的中点,若OE=2,AC+BD=12,则△OAB的周长为10.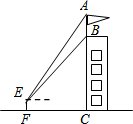 某公司研发一款新型的测角仪,这种测角仪能更精确的测量角度,减少误差.
某公司研发一款新型的测角仪,这种测角仪能更精确的测量角度,减少误差.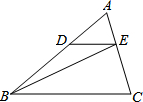 如图,在△ABC中,点D、E分别是AB、AC上的点,DE∥BC,S△ADE:S△BDE=2:3,若S△BEC=15,则S△ABC=( )
如图,在△ABC中,点D、E分别是AB、AC上的点,DE∥BC,S△ADE:S△BDE=2:3,若S△BEC=15,则S△ABC=( )