题目内容
13.不等式$\left\{\begin{array}{l}\frac{1}{2}x+1≥0\\ 1-x>0\end{array}\right.$的正整数解是不存在.分析 此题可先根据一元一次不等式组解出x的取值,根据x是整数解得出x的可能取值.
解答 解:$\left\{\begin{array}{l}{\frac{1}{2}x+1≥0①}\\{1-x>0②}\end{array}\right.$,
解①得:x≥-2,
解②得:x<1,
则不等式组的解集是:-2≤x<1,
则正整数解不存在,
故答案为不存在.
点评 本题考查了不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
4.在下列各式①$\frac{1}{2}$(1-x);②$\frac{2x}{π-3}$;③$\frac{{x}^{2}-{y}^{2}}{2}$;④$\frac{3}{x+y}$;⑤$\frac{5{y}^{2}}{x}$中,是分式有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
3.点P位于第一象限,距y轴3个单位长度,距离x轴4个单位长度,则点P坐标是( )
| A. | (-3,4) | B. | (3,4) | C. | (-4,3) | D. | (4,3) |
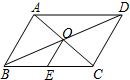 如图,在?ABCD中,对角线AC、BD交于点O,E是BC边上的中点,若OE=2,AC+BD=12,则△OAB的周长为10.
如图,在?ABCD中,对角线AC、BD交于点O,E是BC边上的中点,若OE=2,AC+BD=12,则△OAB的周长为10.