题目内容
17.若x,y都是实数,且y=$\sqrt{x-4}+\sqrt{4-x}$+1,求$\sqrt{x}$+3y的值.分析 首先根据二次根式有意义的条件可得:$\left\{\begin{array}{l}{x-4≥0}\\{4-x≥0}\end{array}\right.$,解不等式组可得x=4,然后再代入y=$\sqrt{x-4}+\sqrt{4-x}$+1可得y的值,进而可得$\sqrt{x}$+3y的值.
解答 解:由题意得:$\left\{\begin{array}{l}{x-4≥0}\\{4-x≥0}\end{array}\right.$,
解得:x=4,
则y=1,
$\sqrt{x}$+3y=2+3=5.
点评 此题主要考查了二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数.

练习册系列答案
相关题目
12.三个数,-π,-3.14,-$\sqrt{3}$的大小关系正确的是( )
| A. | -π<-3.14<-$\sqrt{3}$ | B. | -3.14<-π<-$\sqrt{3}$ | C. | -3.14<-$\sqrt{3}$<-π | D. | -$\sqrt{3}$<-π<-3.14 |
7.△ABC≌△DEF,A与D对应,B与E对应,∠A=32°,∠B=68°,则∠F为( )
| A. | 100° | B. | 80° | C. | 32° | D. | 68° |
 如图所示的一块地,∠ADC=90°,AD=3m,CD=4m,AB=13m,BC=12m,则这块地的面积是36m2.
如图所示的一块地,∠ADC=90°,AD=3m,CD=4m,AB=13m,BC=12m,则这块地的面积是36m2.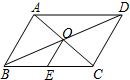 如图,在?ABCD中,对角线AC、BD交于点O,E是BC边上的中点,若OE=2,AC+BD=12,则△OAB的周长为10.
如图,在?ABCD中,对角线AC、BD交于点O,E是BC边上的中点,若OE=2,AC+BD=12,则△OAB的周长为10. 某公司研发一款新型的测角仪,这种测角仪能更精确的测量角度,减少误差.
某公司研发一款新型的测角仪,这种测角仪能更精确的测量角度,减少误差.