题目内容
11.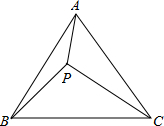 已知,如图,P为等边三角形ABC内一点,PA=3,PB=4,PC=5,求△ABC的面积.
已知,如图,P为等边三角形ABC内一点,PA=3,PB=4,PC=5,求△ABC的面积.
分析 将△BPC绕点B逆时针旋转60°得△BEA,根据旋转的性质得BE=BP=4,AE=PC=5,∠PBE=60°,则△BPE为等边三角形,得到PE=PB=4,∠BPE=60°,在△AEP中,AE=5,延长BP,作AF⊥BP于点FAP=3,PE=4,根据勾股定理的逆定理可得到△APE为直角三角形,且∠APE=90°,即可得到∠APB的度数,在直角△APF中利用三角函数求得AF和PF的长,则在直角△ABF中利用勾股定理求得AB的长,进而求得三角形ABC的面积.
解答 解:∵△ABC为等边三角形,
∴BA=BC,
可将△BPC绕点B逆时针旋转60°得△BEA,
连EP,且延长BP,作AF⊥BP于点F.如图,
∴BE=BP=4,AE=PC=5,∠PBE=60°,
∴△BPE为等边三角形,
∴PE=PB=4,∠BPE=60°,
在△AEP中,AE=5,AP=3,PE=4,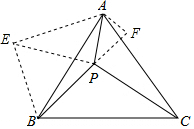
∴AE2=PE2+PA2,
∴△APE为直角三角形,且∠APE=90°,
∴∠APB=90°+60°=150°.
∴∠APF=30°,
∴在直角△APF中,AF=$\frac{1}{2}$AP=$\frac{3}{2}$,PF=$\frac{\sqrt{3}}{2}$AP=$\frac{3\sqrt{3}}{2}$.
∴在直角△ABF中,AB2=BF2+AF2=(4+$\frac{3\sqrt{3}}{2}$)2+($\frac{3}{2}$)2=25+12$\sqrt{3}$.
则△ABC的面积是$\frac{\sqrt{3}•A{B}^{2}}{4}$=$\frac{\sqrt{3}(25+12\sqrt{3})}{4}$=$\frac{25\sqrt{3}+36}{4}$.
点评 本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了等边三角形的判定与性质以及勾股定理的逆定理.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案| A. | 2cm、4cm、5cm | B. | 1cm、1cm、$\sqrt{2}$cm | C. | 1cm、2cm、2cm | D. | $\sqrt{3}$cm、2cm、$\sqrt{5}$cm |
| A. | (-3,4) | B. | (3,4) | C. | (-4,3) | D. | (4,3) |
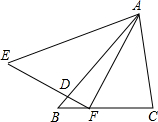 如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )
如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )①∠AFC=∠C;②DF=CF;③△ADE∽△FDB;④∠BFD=∠CAF.
| A. | 只有①③ | B. | 只有①④ | C. | 只有③④ | D. | 只有①③④ |
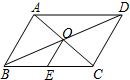 如图,在?ABCD中,对角线AC、BD交于点O,E是BC边上的中点,若OE=2,AC+BD=12,则△OAB的周长为10.
如图,在?ABCD中,对角线AC、BD交于点O,E是BC边上的中点,若OE=2,AC+BD=12,则△OAB的周长为10.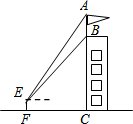 某公司研发一款新型的测角仪,这种测角仪能更精确的测量角度,减少误差.
某公司研发一款新型的测角仪,这种测角仪能更精确的测量角度,减少误差.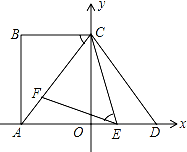 如图,在平面直角坐标系中,点A、C分别在x轴、y轴上,四边形ABCO为矩形,AB=16,点D与点A关于y轴对称,tan∠ACB=$\frac{4}{3}$,∠CDE=∠CAO,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
如图,在平面直角坐标系中,点A、C分别在x轴、y轴上,四边形ABCO为矩形,AB=16,点D与点A关于y轴对称,tan∠ACB=$\frac{4}{3}$,∠CDE=∠CAO,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.