题目内容
7.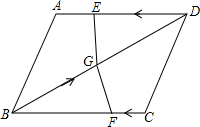 如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.
如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.(1)试证明:AD∥BC.
(2)在移动过程中,小明发现当点G的运动速度取某个值时,有△DEG与△BFG全等的情况出现,请你探究当点G的运动速度取哪些值时,△DEG与△BFG全等.
分析 (1)由AD=BC=8,AB=CD,BD为公共边,所以可证得△ABD≌△CDB,所以可知∠ADB=∠CBD,所以AD∥BC;
(2)设运动时间为t,点G的运动速度为v,根据全等三角形的性质进行解答即可.
解答 (1)证明:在△ABD和△CDB中
$\left\{\begin{array}{l}{AD=BC}\\{AB=CD}\\{BD=DB}\end{array}\right.$,
∴△ABD≌△CDB,
∴∠ADB=∠CBD,
∴AD∥BC;
(2)解:设运动时间为t,点G的运动速度为v,
当0<t≤$\frac{4}{3}$时,若△DEG≌△BFG,则$\left\{\begin{array}{l}DE=BF\\ DG=BG\end{array}$,
∴$\left\{\begin{array}{l}t=4-3t\\ 6-BG=BG\end{array}$,
∴$\left\{\begin{array}{l}t=1\\ BG=3\end{array}$,
∴v=3;
若△DEG≌△BGF,则$\left\{\begin{array}{l}DE=BG\\ DG=BF\end{array}$,
∴$\left\{\begin{array}{l}t=BG\\ 6-BG=4-3t\end{array}$,
∴$\left\{\begin{array}{l}t=-1\\ BG=-1\end{array}$ (舍去);
当$\frac{4}{3}$<t≤$\frac{8}{3}$时,若△DEG≌△BFG,则$\left\{\begin{array}{l}DE=BF\\ DG=BG\end{array}$,
∴$\left\{\begin{array}{l}t=3t-4\\ 6-BG=BG\end{array}$,
∴$\left\{\begin{array}{l}t=2\\ BG=3\end{array}$,
∴v=$\frac{3}{2}$;
若△DEG≌△BGF,则$\left\{\begin{array}{l}DE=BG\\ DG=BF\end{array}$,
∴$\left\{\begin{array}{l}t=BG\\ 6-BG=3t-4\end{array}$,
∴$\left\{\begin{array}{l}t=\frac{5}{2}\\ BG=\frac{5}{2}\end{array}$,
∴v=1.
综上,点G的速度为3或$\frac{3}{2}$或1.
点评 本题主要考查三角形全等的判定和性质,第(2)题解题的关键是利用好三角形全等解得.

 中考解读考点精练系列答案
中考解读考点精练系列答案| A. | $\frac{4}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
| 停靠站 | 起点站 | 中间 第1站 | 中间 第2站 | 中间 第3站 | 中间 第4站 | 中间 第5站 | 中间 第6站 | 终点站 |
| 上下车人数 | +21 | -3 +8 | -4 +2 | 0 +4 | -7 +1 | -9 +6 | -7 0 | -12 |
(2)中间的6个站中,第6站没有人上车,第3站没有人下车;
(3)中间第二站开车时车上人数是24人,第五站停车时车上人数是22人;
(4)从表中你还能知道的一个信息是起点站上车21人.
| A. | 32=(-3)2 | B. | 33=(-3)3 | C. | -32=|-32| | D. | (-3)3=|(-3)3| |
 如图,已知AB=AD,且AC平分∠BAD,求证:BC=DC.
如图,已知AB=AD,且AC平分∠BAD,求证:BC=DC.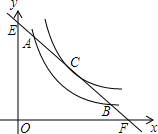 如图,直线y=-x+m与y=$\frac{4}{x}$只有唯一公共点C,与y=$\frac{k}{x}$交于A、B,且AC=$\frac{3}{2}$$\sqrt{2}$,求k.
如图,直线y=-x+m与y=$\frac{4}{x}$只有唯一公共点C,与y=$\frac{k}{x}$交于A、B,且AC=$\frac{3}{2}$$\sqrt{2}$,求k.