题目内容
2.某交警大队的一辆警车沿着一条南北方向的公路巡视,某天早晨从A地出发,晚上到达B地,约定向北为正方向,当天行驶记录如下:(单位:千米)+8.3,-9.5,+7.1,-12,-4.2,+13,-6.8,-8.5
问:(1)B地在A地哪个方向?相距多远?
(2)若该警车每千米耗油O.2升,那么该天共耗油多少升?
(3)若油箱中有油12升,中途是否需要加油?如果需要,至少加多少升?请说明理由.
分析 (1)把所有行驶记录相加,可判断最终位置;
(2)先算出警车行驶的路程,然后算出耗油量;
(3)耗油量与油箱中的油比较,可判断是否需要加油.
解答 解:(1)8.3-9.5+7.1-12-4.2+13-6.8-8.5=-12.6(千米).
答:B在A地的南方,相距12.6千米.
(2)|8.3|+|-9.5|+|+7.1|+|-12|+|-4.2|+|+13|+|-6.8|+|-8.5|=69.4(千米),
69.4×0.2=13.88(升).
答:共耗油13.88升.
(3)13.88-12=1.88(升).
答:需要加油,需要加1.88升油.
点评 本题考查了正数与负数、有理数的加法、利用正负号的意义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17. 如图,⊙O中,$\widehat{CA}=\widehat{CB}$,BD⊥AC于D,OC交BD于E.
如图,⊙O中,$\widehat{CA}=\widehat{CB}$,BD⊥AC于D,OC交BD于E.
(1)求证:∠BEO=∠A;
(2)若AB=4$\sqrt{2}$,OE=1,求⊙O的半径长.
 如图,⊙O中,$\widehat{CA}=\widehat{CB}$,BD⊥AC于D,OC交BD于E.
如图,⊙O中,$\widehat{CA}=\widehat{CB}$,BD⊥AC于D,OC交BD于E.(1)求证:∠BEO=∠A;
(2)若AB=4$\sqrt{2}$,OE=1,求⊙O的半径长.
12. 如图,笑笑书上的三角形被墨迹污损了一部分,但是笑笑根据所学知识画出一个与书本上完全一样的三角形,那么这两个三角形全等的依据不可能是( )
如图,笑笑书上的三角形被墨迹污损了一部分,但是笑笑根据所学知识画出一个与书本上完全一样的三角形,那么这两个三角形全等的依据不可能是( )
 如图,笑笑书上的三角形被墨迹污损了一部分,但是笑笑根据所学知识画出一个与书本上完全一样的三角形,那么这两个三角形全等的依据不可能是( )
如图,笑笑书上的三角形被墨迹污损了一部分,但是笑笑根据所学知识画出一个与书本上完全一样的三角形,那么这两个三角形全等的依据不可能是( )| A. | SSS | B. | ASA | C. | AAS | D. | SAS |
 如图,AE⊥BC,DF⊥BC,E,F是垂足,且AE=DF,AB=DC,求证:∠ABC=∠DCB.
如图,AE⊥BC,DF⊥BC,E,F是垂足,且AE=DF,AB=DC,求证:∠ABC=∠DCB. 如图,⊙0的半径为R,弦AB=a,弦BC∥0A,求AC的长.
如图,⊙0的半径为R,弦AB=a,弦BC∥0A,求AC的长.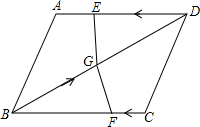 如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.
如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.