题目内容
17.已知$\frac{M}{2x+1}$-$\frac{N}{2x+3}$=$\frac{4x+8}{(2x+1)(2x+3)}$,其中M,N为实数,则M+N的值为4.分析 已知等式左边通分并利用同分母分式的减法法则计算,再利用分式相等的条件求出M与N的值,即可确定出M+N的值.
解答 解:已知等式整理得:$\frac{(2x+3)M-(2x+1)N}{(2x+1)(2x+3)}$=$\frac{4x+8}{(2x+1)(2x+3)}$,
可得2M-2N=4,3M-N=8,
解得:M=3,N=1,
则M+N=3+1=4,
故答案为:4
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
5.下列各式中,属于分式的是( )
| A. | -$\frac{3}{5}$ | B. | $\frac{x{y}^{2}}{4}$ | C. | 6m2n3 | D. | $\frac{{b}^{2}}{a}$ |
12. 如图,笑笑书上的三角形被墨迹污损了一部分,但是笑笑根据所学知识画出一个与书本上完全一样的三角形,那么这两个三角形全等的依据不可能是( )
如图,笑笑书上的三角形被墨迹污损了一部分,但是笑笑根据所学知识画出一个与书本上完全一样的三角形,那么这两个三角形全等的依据不可能是( )
 如图,笑笑书上的三角形被墨迹污损了一部分,但是笑笑根据所学知识画出一个与书本上完全一样的三角形,那么这两个三角形全等的依据不可能是( )
如图,笑笑书上的三角形被墨迹污损了一部分,但是笑笑根据所学知识画出一个与书本上完全一样的三角形,那么这两个三角形全等的依据不可能是( )| A. | SSS | B. | ASA | C. | AAS | D. | SAS |
6.下列各组数中,数值相等的是( )
| A. | $\frac{{3}^{2}}{4}$和$(\frac{3}{4})^{2}$ | B. | -12013和(-1)2015 | C. | -32和(-3)2 | D. | -$\frac{{2}^{2}}{3}$和$\frac{(-2)^{2}}{3}$ |
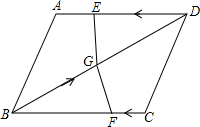 如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.
如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动. 如图,已知半圆的圆心为O,点C是半圆上的一点,过点C作CD⊥AB于D,连接AC,将△ACD沿AC翻折得到△ACD,AD与$\widehat{AC}$交于点E.
如图,已知半圆的圆心为O,点C是半圆上的一点,过点C作CD⊥AB于D,连接AC,将△ACD沿AC翻折得到△ACD,AD与$\widehat{AC}$交于点E.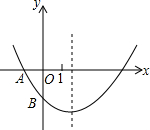 如图,抛物线y=ax2+bx+c交x轴的负半轴于点A,交y轴的负半轴于点B,若OA=OB,则a的取值范围是0<a<1.
如图,抛物线y=ax2+bx+c交x轴的负半轴于点A,交y轴的负半轴于点B,若OA=OB,则a的取值范围是0<a<1.