题目内容
 如图由等腰直角三角形组成,其中第一个直角三角形的腰长为1cm,
如图由等腰直角三角形组成,其中第一个直角三角形的腰长为1cm,(1)求第4个直角三角形的直角边长;
(2)猜出第n个直角三角形的直角边长.
(3)写出当n=10时渐开线(即实线的长之和)的长.
考点:等腰直角三角形
专题:规律型
分析:(1)根据勾股定理先求出①的斜边,再逐步求出③三角形的斜边即可;
(2)根据(1)观察的规律猜出第n个直角三角形的直角边长为
(n-1);
(3)分别求得这10个等腰直角三角形的直角边以及最后一个三角形的斜边,把它们的值相加即可.
(2)根据(1)观察的规律猜出第n个直角三角形的直角边长为
| 2 |
(3)分别求得这10个等腰直角三角形的直角边以及最后一个三角形的斜边,把它们的值相加即可.
解答:解:(1)如图: 根据勾股定理,
根据勾股定理,
②的直角边为a=
=
;
③的直角边为b=
=2;
④的直角边边为c=
=2
;
所以第4个直角三角形的直角边长为2
;
(2)根据(1)猜出第n个直角三角形的直角边长为
(n-1);
(3)由于①的直角边为1,②的直角边为
,③的直角边为2,④的直角边为2
,⑤的直角边为4,⑥的直角边为4
,⑥的直角边为8,⑦的直角边为8
,⑧的直角边为16,⑨的直角边为16
,第10个直角三角形的直角边为32,斜边为32
;
所以当n=10时渐开线(即实线的长之和)的长为:2(1+
+2+2
+4+4
+8+8
+16+16
+32)+32
=126+94
;
 根据勾股定理,
根据勾股定理,②的直角边为a=
| 12+12 |
| 2 |
③的直角边为b=
(
|
④的直角边边为c=
| 22+22 |
| 2 |
所以第4个直角三角形的直角边长为2
| 2 |
(2)根据(1)猜出第n个直角三角形的直角边长为
| 2 |
(3)由于①的直角边为1,②的直角边为
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
所以当n=10时渐开线(即实线的长之和)的长为:2(1+
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查了等腰直角三角形,此图称为数学海螺,利用勾股定理是解题的基本思路.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知,菱形的一条对角线与一条边的和是22,和这条边的差是2,若两对角线的长都是整数,则菱形的面积为( )
| A、96 | B、64 | C、60 | D、48 |
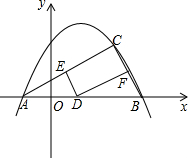 如图,已知抛物线y=-
如图,已知抛物线y=- 如图所示,当小明站立在镜子EF前A处时,他看自己的脚在镜中的像的俯角为45°;如果小华向后退0.6米到B处,这时他看自己的脚在镜中的像的俯角为30°.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据:
如图所示,当小明站立在镜子EF前A处时,他看自己的脚在镜中的像的俯角为45°;如果小华向后退0.6米到B处,这时他看自己的脚在镜中的像的俯角为30°.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据:
 某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下:
某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下: 今年6月,第12届财富全球论坛将在成都召开.某校为了贯彻落实上级有关部门的指示精神,在全校举行了以“财富论坛”为主题的知识竞赛活动,其中九年级(1)、(2)班各派了20人参赛.活动结束后,将这两个班的学生成绩进行了统计,并根据统计数据绘制了如图所示的统计图表.
今年6月,第12届财富全球论坛将在成都召开.某校为了贯彻落实上级有关部门的指示精神,在全校举行了以“财富论坛”为主题的知识竞赛活动,其中九年级(1)、(2)班各派了20人参赛.活动结束后,将这两个班的学生成绩进行了统计,并根据统计数据绘制了如图所示的统计图表.