题目内容
6. (1)将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象,求y2的解析式;
(1)将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象,求y2的解析式;(2)如图,P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线y2交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值.
分析 (1)根据平移规律“左加右减,上加下减”的规律即可写出函数解析式.
(2)设A(t,t),B(t,2t2-8t+8),则AB=|t-(2t2-8t+8)|=|2t2-9t+8|,当△ABP是以点A为直角顶点的等腰直角三角形时,则∠PAB=90°,PA=AB=|t-2|;当△ABP是以点B为直角顶点的等腰直角三角形时,则∠PBA=90°,PB=AB=|t-2|;分别列方程求k的值.
解答 解:(1)∵抛物线y2的图象是由抛物线y1=2x2向右平移2个单位得到,
∴y2=2(x-2)2.
(2)∵y=2(x-2)2
∴y=2x2-8x+8,
∵直线x=t分别与直线y=x、抛物线y=2x2-8x+8交于点A、B两点,
∴设A(t,t),B(t,2t2-8t+8),AB=|t-(2t2-8t+8)|=|2t2-9t+8|,
①当△ABP是以点A为直角顶点的等腰直角三角形时,∠PAB=90°,此时PA=AB=|t-2|,
即|2t2-9t+8|=|t-2|,
∴2t2-9t+8=t-2,或2t2-9t+8=2-t,
解得t=$\frac{5±\sqrt{5}}{2}$或1或3;
②当△ABP是以点B为直角顶点的等腰直角三角形时,则∠PBA=90°,此时PB=AB=|t-2|,结果同上.
故答案为:$\frac{5±\sqrt{5}}{2}$或1或3.
点评 本题考查了二次函数的综合运用.关键是根据函数解析式表示A、B两点坐标,再表示线段AB,根据题意,列方程求解,属于中考常考题型.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
16.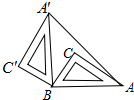 如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )
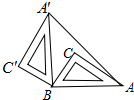 如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )| A. | 10$\sqrt{2}$ | B. | 10 | C. | 20 | D. | 5$\sqrt{2}$ |
17.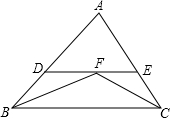 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.若BD+CE=2013,则线段DE的长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.若BD+CE=2013,则线段DE的长为( )
 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.若BD+CE=2013,则线段DE的长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.若BD+CE=2013,则线段DE的长为( )| A. | 2014 | B. | 2011 | C. | 2012 | D. | 2013 |
14.若|a|=8,则a的值是( )
| A. | -8 | B. | 8 | C. | ±8 | D. | ±$\frac{1}{8}$ |
1. 如图,在?ABCD中,AC与BD相交于点O,点E是BC边的中点,AB=2,则OE的长为( )
如图,在?ABCD中,AC与BD相交于点O,点E是BC边的中点,AB=2,则OE的长为( )
 如图,在?ABCD中,AC与BD相交于点O,点E是BC边的中点,AB=2,则OE的长为( )
如图,在?ABCD中,AC与BD相交于点O,点E是BC边的中点,AB=2,则OE的长为( )| A. | 2 | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |

 如图,已知点A、B、C在⊙O上,且AB=AC,∠BAC=40°,BD为⊙O的直径,则∠ADB=70°.
如图,已知点A、B、C在⊙O上,且AB=AC,∠BAC=40°,BD为⊙O的直径,则∠ADB=70°.