题目内容
20.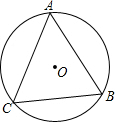 如图,⊙O的半径为2,$\widehat{AB}=\widehat{AC}$,∠A=56°,则$\widehat{AC}$的长为$\frac{62}{45}$π.
如图,⊙O的半径为2,$\widehat{AB}=\widehat{AC}$,∠A=56°,则$\widehat{AC}$的长为$\frac{62}{45}$π.
分析 连接OA,OC,根据圆周角定理以及三角形内角和定理得出∠B=62°,∠AOC=124°,再根据弧长的计算公式即可求解.
解答  解:连接OA,OC.
解:连接OA,OC.
∵$\widehat{AB}=\widehat{AC}$,
∴∠B=∠C,
∵∠A=56°,
∴∠B=$\frac{1}{2}$(180°-56°)=62°,
∴∠AOC=124°,
∴$\widehat{AC}$的长为:$\frac{124π×2}{180}$=$\frac{62}{45}$π.
故答案为$\frac{62}{45}$π.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,同时考查了弧长公式:l=$\frac{nπR}{180}$(弧长为l,圆心角度数为n,圆的半径为R)以及三角形内角和定理,注意:在弧长的计算公式中,n是表示1°的圆心角的倍数,n和180都不要带单位.

练习册系列答案
相关题目
10.已知△ABC的六个元素,下面甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是( )


| A. | 只有乙 | B. | 只有丙 | C. | 甲和乙 | D. | 乙和丙 |
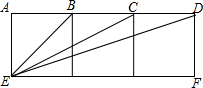 如图由三个边长为1正方形拼成矩形AEFD,求证:△BCE∽△BED.
如图由三个边长为1正方形拼成矩形AEFD,求证:△BCE∽△BED.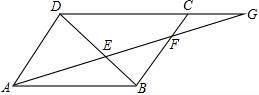 如图,?ABCD中,点G在DC的延长线上,AG分别交BD、BC于点E、F,图中△ABE∽△GDE,与△ADE相似的三角形有△FBE,与△CFG相似的三角形有△DAG,△BFA.
如图,?ABCD中,点G在DC的延长线上,AG分别交BD、BC于点E、F,图中△ABE∽△GDE,与△ADE相似的三角形有△FBE,与△CFG相似的三角形有△DAG,△BFA.