题目内容
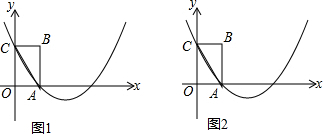
8．如图，在平面直角坐标系中，矩形OABC的边OA、OC分别位于x轴、y轴上，经过A、C两点的抛物线交x轴于另一点D，连接AC，请你只用无刻度的直尺按要求画图．（1）在图1中的抛物线上，画出点E，使DE=AC；
（2）在图2中的抛物线上，画出抛物线的顶点F．
分析 （1）延长CB交抛物线于点E，则C、E两点的纵坐标相等，根据抛物线的对称性即可得；
（2）由（1）知CE∥AD、AC=DE知四边形ADEC是等腰梯形，延长CA、ED交于点P知△PCE为等腰三角形，连接CD、AE交于点Q，连接PQ交抛物线于点F，根据等腰梯形和等腰三角形的轴对称性即可得．
解答 解：（1）如图1，延长CB交抛物线于点E，点E即为所求；
（2）如图2，
延长CA、ED交于点P，连接CD、AE交于点Q，连接PQ交抛物线于点F，点F即为所求．
点评 本题主要考查抛物线与x轴的交点、等腰梯形和等腰三角形的性质，熟练掌握抛物线、等腰梯形及等腰三角形的轴对称性是解题的关键．
练习册系列答案
一课一练课时达标系列答案
相关题目
16．
如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连接BD、DP，BD与CF相交于点H，给出下列结论：
①BE=2AE；②△DFP∽△BPH；③△PFD∽△PDB；④DP2=PH•PC
其中正确的是（ ）
如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连接BD、DP，BD与CF相交于点H，给出下列结论：①BE=2AE；②△DFP∽△BPH；③△PFD∽△PDB；④DP2=PH•PC
其中正确的是（ ）
| A． | ①②③④ | B． | ②③ | C． | ①②④ | D． | ①③④ |
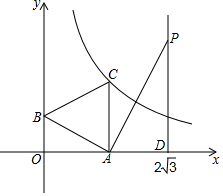如图，一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B，以线段AB为边在第一象限作等边△ABC．
如图，平面直角坐标系中，已知直线y=x上一点P（2，2）C为y轴上一点，连接PC，线段PC绕点P顺时针旋转90°至线段PD，过点D作直线AB⊥x轴，垂足为B，直线AB与直线y=x交于点A，且BD=2AD，连接CD，直线CD与直线y=x交于点Q．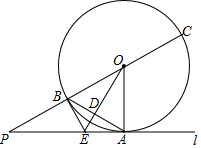
如图，直线1与⊙O相切于点A，点P在直线1上，直线PO交⊙O于点B、C，OD⊥AB，垂足为D，交PA于点E．
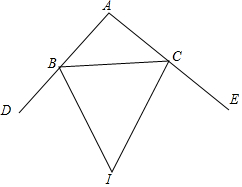如图，BI，CI分别平分△ABC的外角∠DBC和∠ECB，
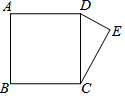如图，正方形ABCD的边长为13，以CD为斜边向外作Rt△CDE．若点A到CE的距离为17，则CE=12或5．
18．已知抛物线y=x2+bx+c的对称轴为x=1．且与x轴交于A、B两点，AB=2．若关于x的一元二次方程x2+bx+c=t（t为实数）在-2≤x＜$\frac{7}{2}$的范围囤内有实数解．t的取值范围是（ ）
| A． | 1≤t≤$\frac{21}{4}$ | B． | -2≤t≤3 | C． | -1≤t＜8 | D． | -2≤t＜8 |