题目内容
15.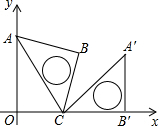 将一个含45°角的三角板ABC如图摆放在平面直角坐标系中,将其绕点C顺时针旋转75°,点B的对应点B′恰好落在x轴上,若点C的坐标为(1,0),则点B′的坐标为(1+$\sqrt{2}$,0).
将一个含45°角的三角板ABC如图摆放在平面直角坐标系中,将其绕点C顺时针旋转75°,点B的对应点B′恰好落在x轴上,若点C的坐标为(1,0),则点B′的坐标为(1+$\sqrt{2}$,0).
分析 先求得∠ACO=60°,得出∠OAC=30°,求得AC=20C=2,解等腰直角三角形求得直角边为$\sqrt{2}$,从而求出B′的坐标.
解答 解:如图,∵∠ACB=45°,∠BCB′=75°,
∴∠ACB′=120°,
∴∠ACO=60°,
∴∠OAC=30°,
∴AC=2OC,
∵点C的坐标为(1,0),
∴OC=1,
∴AC=2OC=2,
∵△ABC是等腰直角三角形,
∴AB=BC=$\sqrt{2}$,
∴B′C=A′B′=$\sqrt{2}$,
∴OB′=1+$\sqrt{2}$,
∴B′点的坐标为(1+$\sqrt{2}$,0).
点评 此题主要考查了旋转的性质及坐标与图形变换,同时也利用了直角三角形性质,首先利用直角三角形的性质得到有关线段的长度,即可解决问题.

练习册系列答案
相关题目
3. 在一年一度的国家学生体质侧试中,金星中学对全饺2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并制作成统计表,绘制成频数直方图.
在一年一度的国家学生体质侧试中,金星中学对全饺2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并制作成统计表,绘制成频数直方图.
(1)在这个问题中,总体是什么?
(2)直接写出a,b,c,d的值.
(3)补全频数直方图.
(4)初中毕业生体能测试项目成绩评定标准是男生1000m不超过4′20″(即260秒)为合格,你能估计出该校初中男生的1000m的合格人数吗?如果能,请求出合格的人数;如果不能,请说明理由.
 在一年一度的国家学生体质侧试中,金星中学对全饺2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并制作成统计表,绘制成频数直方图.
在一年一度的国家学生体质侧试中,金星中学对全饺2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并制作成统计表,绘制成频数直方图.| 序号 | 范围(单位:秒) | 频数 | 频率 |
| 1 | 170<x≤200 | 5 | 0.1 |
| 2 | 200<x≤230 | 13 | a |
| 3 | 230<x≤260 | 15 | 0.3 |
| 4 | 260<x≤290 | c | d |
| 5 | 290<x≤320 | 5 | 0.1 |
| 6 | 320<x≤350 | 2 | 0.04 |
| 7 | 350<x≤380 | 2 | 0.04 |
| 合计 | b | 1.00 |
(2)直接写出a,b,c,d的值.
(3)补全频数直方图.
(4)初中毕业生体能测试项目成绩评定标准是男生1000m不超过4′20″(即260秒)为合格,你能估计出该校初中男生的1000m的合格人数吗?如果能,请求出合格的人数;如果不能,请说明理由.
10.某市深入实施环境污染整治,去年排放的污水减少了30万吨,将30万用科学记数法表示为( )
| A. | 3.0×105 | B. | 30×104 | C. | 3.0×104 | D. | 3.0×101 |
7.下列各式能用平方差公式进行计算的是( )
| A. | (x-3)(x+1) | B. | (a+2b)(2a-b) | C. | (-a+1)(-a-1) | D. | (x-3)2 |
 如图是一把剪刀,若∠1与∠2互为余角,则∠1=45°.
如图是一把剪刀,若∠1与∠2互为余角,则∠1=45°. 如图所示,∠1=∠DBF,∠3=∠4,且BD=BF
如图所示,∠1=∠DBF,∠3=∠4,且BD=BF