题目内容
4. 如图所示,∠1=∠DBF,∠3=∠4,且BD=BF
如图所示,∠1=∠DBF,∠3=∠4,且BD=BF(1)求证:△ABD≌△CBF;
(2)求证:∠ABC+2∠2=180°.
分析 (1)根据三角形的内角和得到∠1=∠ABC,等量代换得到∠ABC=∠DBF,根据角的和差得到∠ABD=∠CBF,于是得到结论;
(2)根据∠3=∠4,推出A,D,B,C四点共圆,由圆周角定理得到∠2=∠BAC,根据等腰三角形的性质得到∠BAC=∠ACB,然后由三角形的内角和即可得到结论.
解答  证明:(1)∵∠3=∠4,∠AED=∠BEC,
证明:(1)∵∠3=∠4,∠AED=∠BEC,
∴∠1=∠ABC,
∵∠1=∠DBF,
∴∠ABC=∠DBF,
∴∠ABC-∠EBF=∠DBF-∠EBF,
即∠ABD=∠CBF,
在△ABD与△CBF中,
$\left\{\begin{array}{l}{∠3=∠4}\\{∠ABD=∠CBF}\\{BD=BF}\end{array}\right.$,
∴△ABD≌△CBF;
(2)∵∠3=∠4,
∴A,D,B,C四点共圆,
∴∠2=∠BAC,
∵△ABD≌△CBF,
∴AB=BC,
∴∠BAC=∠ACB,
∴∠2=∠BAC=∠ACB,
∵∠ABC+∠BAC+∠ACB=180°,
∴∠ABC+2∠2=180°.
点评 本题考查了全等三角形的判定和性质,四点共圆,圆周角定理,三角形的内角和,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
15.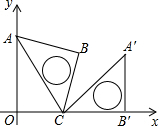 将一个含45°角的三角板ABC如图摆放在平面直角坐标系中,将其绕点C顺时针旋转75°,点B的对应点B′恰好落在x轴上,若点C的坐标为(1,0),则点B′的坐标为(1+$\sqrt{2}$,0).
将一个含45°角的三角板ABC如图摆放在平面直角坐标系中,将其绕点C顺时针旋转75°,点B的对应点B′恰好落在x轴上,若点C的坐标为(1,0),则点B′的坐标为(1+$\sqrt{2}$,0).
 将一个含45°角的三角板ABC如图摆放在平面直角坐标系中,将其绕点C顺时针旋转75°,点B的对应点B′恰好落在x轴上,若点C的坐标为(1,0),则点B′的坐标为(1+$\sqrt{2}$,0).
将一个含45°角的三角板ABC如图摆放在平面直角坐标系中,将其绕点C顺时针旋转75°,点B的对应点B′恰好落在x轴上,若点C的坐标为(1,0),则点B′的坐标为(1+$\sqrt{2}$,0).
12.若a=-0.32,b=-3-2,c=$(-\frac{1}{2})^{-2}$,d=(-$\frac{1}{3}$)0,则它们的大小关系是( )
| A. | a<b<c<d | B. | b<a<d<c | C. | a<d<c<b | D. | c<a<d<b |
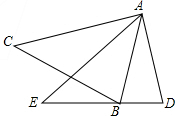 如图,在△ADE中,∠CAE=∠BAD,AC=AE.
如图,在△ADE中,∠CAE=∠BAD,AC=AE.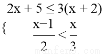
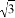 ,坝高BC=10m,则坡面AB的长度是( )
,坝高BC=10m,则坡面AB的长度是( ) 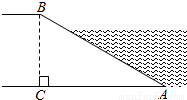
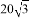 m C.
m C. 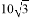 m D. 20m
m D. 20m 和
和 (
( B.
B. 
 D.
D. 