题目内容
14.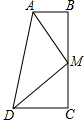 已知:如图,∠C=∠B=90°,M是BC的中点,DM平分∠ADC.
已知:如图,∠C=∠B=90°,M是BC的中点,DM平分∠ADC.(1)若连接AM,则AM是否平分∠DAB?请证明你的结论.
(2)线段AM与DM有怎样的位置关系?请说明理由.
分析 (1)作ME⊥AD于点E,证明△AEM≌△ABM就可以得出∠EAM=∠DAB,从而得出AM平分∠DAB;
(2)由全等可以得出∠DMC=∠DME,∠AME=∠AMB就可以得出∠AMD=90°就可以得出结论.
解答 解:(1)AM是平分∠DAB.
理由:作ME⊥AD于点E,
∴∠AEM=∠DEM=90°.
∵DM平分∠ADC,
∴∠EDM=∠CDM.
∵∠C=∠B=90°,
∴∠B=∠AEM.∠DEM=∠C.
∴ME=MC.
∵M是BC的中点,
∴BM=CM.
∴BM=EM.
在Rt△AEM和Rt△ABM中
$\left\{\begin{array}{l}{AM=AM}\\{EM=BM}\end{array}\right.$,
∴Rt△AEM≌Rt△ABM(HL),
∴∠EAM=∠BAM,∠AME=∠AMB,
∴AM是平分∠DAB;
(2)AM⊥DM.
理由:在Rt△MDE和Rt△MDC中
$\left\{\begin{array}{l}{DM=DM}\\{ME=MC}\end{array}\right.$,
∴Rt△MDE≌Rt△MDC(HL),
∴∠EMD=∠CMD,
∵∠EMD+∠CMD+∠AME+∠AMB=180°
∴2∠EMD+2∠AME=180°,
∴∠EMD+∠AME=90°
∴∠AMD=90°
∴AM⊥DM.
点评 本题考查了中点的定义的运用,角平分线的判定及性质的运用,全等三角形的判定及性质的运用,垂直的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知$\frac{b}{a}$=$\frac{2}{3}$,则$\frac{a}{a+b}$的值是( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
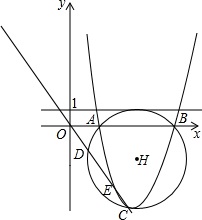 如图,抛物线y=(x+m)2+m,与直线y=-x相交于E,C两点(点E在点C的左边),抛物线与x轴交于A,B两点(点A在点B的左边).△ABC的外接圆⊙H与直线y=-x相交于点D.
如图,抛物线y=(x+m)2+m,与直线y=-x相交于E,C两点(点E在点C的左边),抛物线与x轴交于A,B两点(点A在点B的左边).△ABC的外接圆⊙H与直线y=-x相交于点D.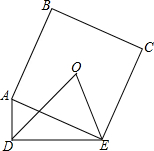 如图,在Rt△ADE中,∠ADE=90°,AD=3cm,DE=5cm,以AE为边向外作正方形ABCE,O为正方形ABCE的中心,则△DOE的面积为10cm2.
如图,在Rt△ADE中,∠ADE=90°,AD=3cm,DE=5cm,以AE为边向外作正方形ABCE,O为正方形ABCE的中心,则△DOE的面积为10cm2.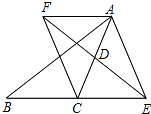 已知,如图,△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF,求证:CF∥AE.
已知,如图,△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF,求证:CF∥AE.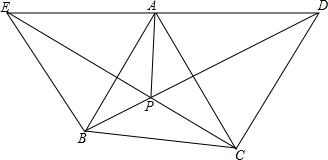 锐角△ABC中,∠BAC=60°,分别以AB,AC为边向外作正△ABE,△ACD,若AP=4,CP=5,则BP=$\frac{16}{5}$.
锐角△ABC中,∠BAC=60°,分别以AB,AC为边向外作正△ABE,△ACD,若AP=4,CP=5,则BP=$\frac{16}{5}$.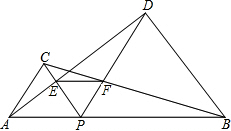 如图所示,P是线段AB上一点,△APC和△BPD都是正三角形,AD与PC交于点E,BC与PD交于点F,连接EF,试探究△PEF的形状.
如图所示,P是线段AB上一点,△APC和△BPD都是正三角形,AD与PC交于点E,BC与PD交于点F,连接EF,试探究△PEF的形状.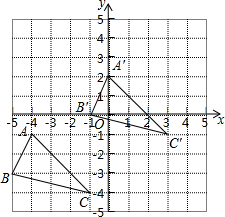 如图,直角坐标系中,A(-4,-1),B(-5,-3),C(-1,-4),将△ABC平移,得到△A′B′C′,且点A的对应点A′的坐标为(0,2).
如图,直角坐标系中,A(-4,-1),B(-5,-3),C(-1,-4),将△ABC平移,得到△A′B′C′,且点A的对应点A′的坐标为(0,2).