题目内容
5.已知$\frac{b}{a}$=$\frac{2}{3}$,则$\frac{a}{a+b}$的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
分析 根据合比性质,可得$\frac{a+b}{a}$的值,再根据反比性质,可得答案.
解答 解:由合比性质,得$\frac{a+b}{a}$=$\frac{2+3}{3}$,
由反比性质,得
$\frac{a}{a+b}$=$\frac{3}{5}$,
故选:A.
点评 本题考查了比例的性质,利用了和比性质:$\frac{a}{b}$=$\frac{c}{d}$⇒$\frac{a+b}{b}$=$\frac{c+d}{d}$,又利用了反比性质:$\frac{a}{b}$=$\frac{c}{d}$⇒$\frac{b}{a}$=$\frac{d}{c}$.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
16.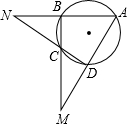 如图,四边形ABCD内接于⊙O,AB、DC延长线交于N,AD、BC的延长线交于M,∠M=40°,∠N=20°,则∠A是( )
如图,四边形ABCD内接于⊙O,AB、DC延长线交于N,AD、BC的延长线交于M,∠M=40°,∠N=20°,则∠A是( )
 如图,四边形ABCD内接于⊙O,AB、DC延长线交于N,AD、BC的延长线交于M,∠M=40°,∠N=20°,则∠A是( )
如图,四边形ABCD内接于⊙O,AB、DC延长线交于N,AD、BC的延长线交于M,∠M=40°,∠N=20°,则∠A是( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
13.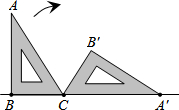 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC的长为7.5cm,那么顶点A从开始到结束所经过的路径长为( )
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC的长为7.5cm,那么顶点A从开始到结束所经过的路径长为( )
 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC的长为7.5cm,那么顶点A从开始到结束所经过的路径长为( )
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC的长为7.5cm,那么顶点A从开始到结束所经过的路径长为( )| A. | 10πcm | B. | 10$\sqrt{3}$πcm | C. | 15πcm | D. | 20πcm |
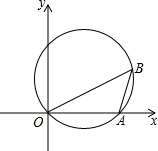 如图,已知点A(8,0),sin∠AB0=$\frac{4}{5}$,抛物线经过点0、A,且顶点在△A0B的外接圆上,则此抛物线的表达式为y=-$\frac{1}{2}$x2+4x.
如图,已知点A(8,0),sin∠AB0=$\frac{4}{5}$,抛物线经过点0、A,且顶点在△A0B的外接圆上,则此抛物线的表达式为y=-$\frac{1}{2}$x2+4x.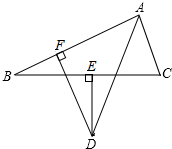 已知△ABC中,AB>AC,∠BAC的平分线与BC的垂直平分线DE交于点D,过点D作DF⊥AB,垂足为F.
已知△ABC中,AB>AC,∠BAC的平分线与BC的垂直平分线DE交于点D,过点D作DF⊥AB,垂足为F.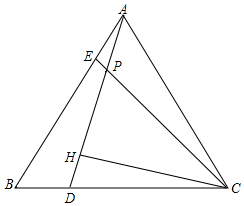 如图,△ABC是等边三角形,D、E分别在BC、AB上,且AE=BD,连接AD、CE交于P,过点C作CH⊥AD于H.
如图,△ABC是等边三角形,D、E分别在BC、AB上,且AE=BD,连接AD、CE交于P,过点C作CH⊥AD于H.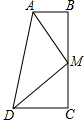 已知:如图,∠C=∠B=90°,M是BC的中点,DM平分∠ADC.
已知:如图,∠C=∠B=90°,M是BC的中点,DM平分∠ADC.