题目内容
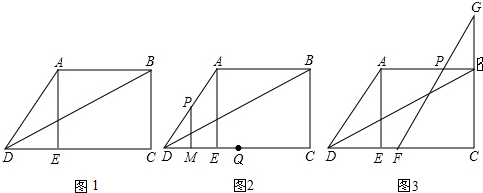
4.如图1,在直角梯形ABCD中,AB∥CD,∠C=90°,AE⊥CD于E,DE=3,AE=4,对角线DB平分∠ADC.(1)求梯形ABCD的面积;
(2)如图2,一动点P从D点出发,以2个单位/秒的速度沿折线DA-AB匀速运动,另一动点Q从E点出发,以1个单位/秒的速度沿EC匀速运动,P、Q同时出发,当Q与C重合时,P、Q停止运动,在点P的运动过程中,过P作PM⊥DC于M,在点P、Q的运动过程中,以PM、MQ为两边作矩形PMQN,使矩形PMQN在直线DC上侧,直线AD右侧,设运动时间为t秒(t>0).在整个运动过程中,设矩形PMQN和CBD重叠部分的面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)如图3,动点P从D点出发,以2个单位/秒的速度沿线段DA运动到A点后,可沿直线AB方向向左或右匀速运动,过点P作PF∥AD交CB的延长线于G点,交CD于F点,在直线AB上是否存在H点,使得△FGH为等腰直角三角形?若存在,求出对应的BH的值;若不存在,请说明理由.
分析 (1)先根据勾股定理得出AD的长,再证明△ADB是等腰三角形,得出AB=AD,最后利用梯形面积公式解答即可;
(2)根据AD,AB,EC的长度,以及P,Q的速度分情况讨论,得出函数关系式并结合自变量的范围解答即可;
(3)根据全等三角形的判定和性质得出△HFW≌△FGC,再利用三角函数求出WF的值后可得BH的值,注意分情况进行分析.
解答 解:在Rt△ADE中,AD=$\sqrt{D{E}^{2}+A{E}^{2}}=5$,
∵AB∥CD,
∴∠ADB=∠CBD,
∵BD平分∠ADC,
∴∠ABD=∠CBD,
∴∠ADB=∠CBD,
∴AB=AD=5,
∵AB∥CD,∠C=90°,AE⊥CD,
∴四边形ABCE为矩形,
∴CE=AB=5,
∴DC=DE+CE=8,
${S}_{梯形ABCD}=\frac{1}{2}(AB+CD)•AE=26$;
(2)∵点P从D点出发,以2个单位/秒的速度沿折线DA-AB匀速运动,动点Q从E点出发,以1个单位/秒的速度沿EC匀速运动,
所以可得三种情况,当矩形在BD下侧时,函数关系式为:$S=-\frac{33}{25}{t}^{2}+\frac{24}{5}t$,此时自变量范围是($0<t≤\frac{15}{11}$);
当矩形在BD上侧,且点P到A点之间时,函数关系式为:$S=-\frac{11}{100}{t}^{2}+\frac{3}{2}t+\frac{9}{4}$,此时自变量的范围是($\frac{15}{11}<t≤\frac{5}{2}$);
当点P在AB之间,且点E刚到达E点时,期间的函数关系式为:$S=-\frac{3}{4}{t}^{2}+\frac{7}{2}t+\frac{5}{4}$,此时自变量的范围是($\frac{5}{2}<t≤5$);
(3)存在,理由如下:
①若∠GFH=90°,过H作HW⊥CD于W,如图1,图2,

∴△HFW≌△FGC,
∴WH=FC=4,WF=CG=$\frac{FC}{tan∠GFC}=\frac{4}{\frac{4}{3}}=3$,
∴BH=WC=WF±CF=7或1;
②若∠FHG=90°,过H作HW⊥CD于W,如图3,图4,

∴△HFW≌△HGB,
∴HW=BH=4,
③若∠FGH=90°,如图5,图6,

∴△CFG≌△BGH,令CF=BG=3x,
∴CG=BH=4x,
∴4x±3x=4,
∴x=$\frac{4}{7}$或x=7,
∴BH=$\frac{16}{7}$或28.
点评 此题考查的是函数和四边形的综合题,难度比较大,关键是勾股定理和矩形的判定,注意动点运动的各种情况,不能漏解.

 阅读快车系列答案
阅读快车系列答案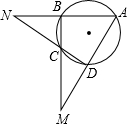 如图,四边形ABCD内接于⊙O,AB、DC延长线交于N,AD、BC的延长线交于M,∠M=40°,∠N=20°,则∠A是( )
如图,四边形ABCD内接于⊙O,AB、DC延长线交于N,AD、BC的延长线交于M,∠M=40°,∠N=20°,则∠A是( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
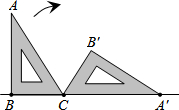 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC的长为7.5cm,那么顶点A从开始到结束所经过的路径长为( )
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC的长为7.5cm,那么顶点A从开始到结束所经过的路径长为( )| A. | 10πcm | B. | 10$\sqrt{3}$πcm | C. | 15πcm | D. | 20πcm |
 如图,在Rt△ABC中,∠C为直角,CD⊥AB于点D,BC=3,AB=5,则BD=$\frac{9}{5}$.
如图,在Rt△ABC中,∠C为直角,CD⊥AB于点D,BC=3,AB=5,则BD=$\frac{9}{5}$.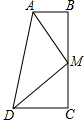 已知:如图,∠C=∠B=90°,M是BC的中点,DM平分∠ADC.
已知:如图,∠C=∠B=90°,M是BC的中点,DM平分∠ADC.