题目内容
11. 如图,在边长为1的正方形ABCD中,将射线AC绕点A按顺时针方向旋转α度(0<α≤360)得到射线AE,点M是点D关于射线AE的对称点,则线段CM长度的最小值为( )
如图,在边长为1的正方形ABCD中,将射线AC绕点A按顺时针方向旋转α度(0<α≤360)得到射线AE,点M是点D关于射线AE的对称点,则线段CM长度的最小值为( )| A. | $\sqrt{2}$-1 | B. | 0.5 | C. | 1 | D. | $\sqrt{2}+1$ |
分析 由轴对称的性质可知AM=AD,故此点M在以A圆心,以AD为半径的圆上,故此当点A、M、C在一条直线上时,CM有最小值.
解答 解:如图所示:连接AM.
∵四边形ABCD为正方形,
∴AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{2}$.
∵点D与点M关于AE对称,
∴AM=AD=1.
∴点M在以A为圆心,以AD长为半径的圆上.
如图所示,当点A、M、C在一条直线上时,CM有最小值.
∴CM的最小值=AC-AM′=$\sqrt{2}$-1.
故选:A.
点评 本题主要考查的是旋转的性质,依据旋转的性质确定出点M运动的轨迹是解题的关键.

练习册系列答案
相关题目
1.下列说法正确的是( )
| A. | 调查重庆市空气质量情况应该采用普查的方式 | |
| B. | A组数据方差$S_A^2=0.03$,B组数据方差$S_B^2=0.2$,则B组数据比A组数据稳定 | |
| C. | 重庆八中明年开运动会一定不会下雨 | |
| D. | 2,3,6,9,5这组数据的中位数是5 |
19.多项式x2-4x-12可以因式分解成( )
| A. | x(x-4)-12 | B. | (x-2)(x+6) | C. | (x+2)(x-6) | D. | (x+3)(x-4) |
6.下列因式分解中正确的是( )
| A. | x2+25=(x+5)(x-5) | B. | 4x2-9y2=(2x+3y)(3x-2y) | ||
| C. | 4x2-6x+1=(2x-3)2 | D. | 2x2-x-6=(x-2)(2x+3) |
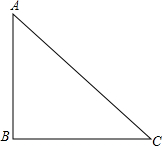 如图,已知,在Rt△ABC中,∠ABC=90°,AB=BC=2.
如图,已知,在Rt△ABC中,∠ABC=90°,AB=BC=2. 如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,∠CBF=20°.
如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,∠CBF=20°.