题目内容
16.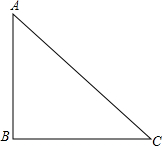 如图,已知,在Rt△ABC中,∠ABC=90°,AB=BC=2.
如图,已知,在Rt△ABC中,∠ABC=90°,AB=BC=2.(1)用尺规作∠A的平分线AD.
(2)角平分线AD交BC于点D,求BD的长.
分析 (1)利用基本作作(作已知角的平分线)作AD平分∠BAC;
(2)作DE⊥AC于E,如图,先判断△ABC为等腰直角三角形得到∠C=45°,则可判断△CDE为等腰直角三角形,则CD=$\sqrt{2}$DE,再根据角平分线的性质得到BD=BE,设BD=x,则CD=$\sqrt{2}$x,然后利用BC=2列方程x+$\sqrt{2}$x=2,再解方程即可.
解答 解:(1)如图,AD为所求;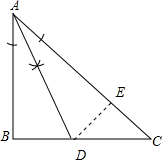
(2)作DE⊥AC于E,如图,
∵∠ABC=90°,AB=BC=2.
∴△ABC为等腰直角三角形,
∴∠C=45°,
∴△CDE为等腰直角三角形,
∴CD=$\sqrt{2}$DE,
∵AD为角平分线,DB⊥AB,DE⊥AC,
∴BD=BE,
设BD=x,则CD=$\sqrt{2}$x,
∴x+$\sqrt{2}$x=2,
∴x=2($\sqrt{2}$-1)=2$\sqrt{2}$-2,
即BD的长为2$\sqrt{2}$-2.
点评 本题考查了基本作图:熟练掌握5个基本作图.掌握角平分线的性质定理和等腰直角三角形的判定与性质是解决(2)小题的关键.

练习册系列答案
相关题目
6.下列各组的两个数中,运算后结果相等的是( )
| A. | 23和32 | B. | -23和(-2)3 | C. | -42和(-4)2 | D. | (-$\frac{2}{3}$)3和-$\frac{{2}^{3}}{3}$ |
7.下列六种说法正确的个数是( )
①无限小数都是无理数;
②正数、负数统称实数;
③无理数的相反数还是无理数;
④无理数与无理数的和一定还是无理数;
⑤无理数与有理数的和一定是无理数;
⑥无理数与有理数的积一定仍是无理数.
①无限小数都是无理数;
②正数、负数统称实数;
③无理数的相反数还是无理数;
④无理数与无理数的和一定还是无理数;
⑤无理数与有理数的和一定是无理数;
⑥无理数与有理数的积一定仍是无理数.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.一个样本有若干个数据,分为5组,第三组的频数为12,频率为15%,样本容量是( )
| A. | 60 | B. | 75 | C. | 80 | D. | 180 |
11. 如图,在边长为1的正方形ABCD中,将射线AC绕点A按顺时针方向旋转α度(0<α≤360)得到射线AE,点M是点D关于射线AE的对称点,则线段CM长度的最小值为( )
如图,在边长为1的正方形ABCD中,将射线AC绕点A按顺时针方向旋转α度(0<α≤360)得到射线AE,点M是点D关于射线AE的对称点,则线段CM长度的最小值为( )
 如图,在边长为1的正方形ABCD中,将射线AC绕点A按顺时针方向旋转α度(0<α≤360)得到射线AE,点M是点D关于射线AE的对称点,则线段CM长度的最小值为( )
如图,在边长为1的正方形ABCD中,将射线AC绕点A按顺时针方向旋转α度(0<α≤360)得到射线AE,点M是点D关于射线AE的对称点,则线段CM长度的最小值为( )| A. | $\sqrt{2}$-1 | B. | 0.5 | C. | 1 | D. | $\sqrt{2}+1$ |