题目内容
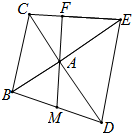 如图,△ABC、△DAE都是等腰直角三角形,M为BD中点,M、A、F共线,求证:①AF⊥CE;②CE=2DM.
如图,△ABC、△DAE都是等腰直角三角形,M为BD中点,M、A、F共线,求证:①AF⊥CE;②CE=2DM.考点:全等三角形的判定与性质,正方形的性质
专题:
分析:①易证△CAE≌△BAD,可得CE=BD,∠AEC=∠ADB,根据∠DAM+∠BAM=90°即可求得∠EAF+∠AEC=90°,即可解题;
②根据全等三角形对应边相等的性质可得CE=BD,再根据BD=2DM即可解题.
②根据全等三角形对应边相等的性质可得CE=BD,再根据BD=2DM即可解题.
解答:证明:①∵在△CAE和△BAD中,
,
∴△CAE≌△BAD,(SAS)
∴CE=BD,∠AEC=∠ADB,
∵M是BD中点,
∴DM=AM=BM,
∴∠ADB=∠DAM,
∵∠DAM+∠BAM=90°,∠BAM=∠EAF,
∴∠EAF+∠AEC=90°,
∴∠AFE=90°,即AF⊥CE;
②∵CE=BD,BD=2DM,
∴CE=2DM.
|
∴△CAE≌△BAD,(SAS)
∴CE=BD,∠AEC=∠ADB,
∵M是BD中点,
∴DM=AM=BM,
∴∠ADB=∠DAM,
∵∠DAM+∠BAM=90°,∠BAM=∠EAF,
∴∠EAF+∠AEC=90°,
∴∠AFE=90°,即AF⊥CE;
②∵CE=BD,BD=2DM,
∴CE=2DM.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△CAE≌△BAD是解题的关键.

练习册系列答案
相关题目
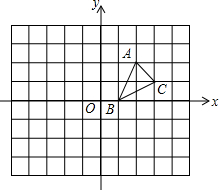 如图,在建立了平面直角坐标系的正方形网格中,A(2,2),B(1,0),C(3,1)
如图,在建立了平面直角坐标系的正方形网格中,A(2,2),B(1,0),C(3,1) 如图,∠1=∠2,∠3=∠4,∠A=80°,求∠BOC的度数.
如图,∠1=∠2,∠3=∠4,∠A=80°,求∠BOC的度数.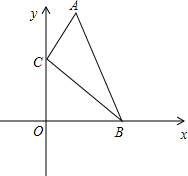 如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.
如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.