题目内容
7.为了解我县九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:40分;B:39-35分;C:34-30分;D:29-20分;E:19-0分)统计如表:| 分数段 | 人数(人) | 频率 |
| A | 48 | 0.48 |
| B | a | 0.32 |
| C | b | 0.10 |
| D | c | d |
| E | e | 0.05 |
(1)在统计表中,a的值为32,c的值为0.05;
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数”.请问甲同学体育成绩应在什么分数段内?B(填相应分数段的字母);
(3)若把成绩在35分以上(含35分)定位优秀,则我县今年8500名九年级学生中体育成绩为优秀的学生人数约有多少名?
分析 (1)根据A组人数是48对应的频率是0.48即可求得总人数,然后利用百分比的意义求得a和c的值;
(2)根据中位数的定义即可确定;
(3)利用8500乘以对应的百分比即可求解.
解答 解:(1)抽取的总人数是:48÷0.48=100(人),
则a=100×0.32=32,
d=1-0.48-0.32-0.10-0.05=0.05,
则c=100×0.05=5;
(2)甲同学体育成绩应在B分数段.
故答案是:B;
(3)8500×(0.48+0.32)=6800.
则体育成绩为优秀的学生人数约是6800名.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力.同时考查中位数的求法:给定n个数据,按从小到大排序,如果n为奇数,位于中间的那个数就是中位数;如果n为偶数,位于中间两个数的平均数就是中位数.任何一组数据,都一定存在中位数的,但中位数不一定是这组数据量的数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.我市农业结构调整取得了巨大成功,今年水果又喜获丰收,某果园组织30辆汽车装运A、B、C三种水果共84t到外地销售,规定每辆汽车只装运一种水果,且必须装满;又装运每种水果的汽车不少于4辆;同时,装运的B种水果的汽车辆数不超过装运的A、C两种水果的汽车辆数之和.
(1)设用x辆汽车装运A种水果,用y辆汽车装运B种水果,根据下表提供的信息,求y与x之间的函数关系式并直接写出自变量x的取值范围;
(2)设此次外销活动的利润为Q(百元),求Q与x之间的函数关系式,请你提出一个获得最大利润时的车辆分配方案.
(1)设用x辆汽车装运A种水果,用y辆汽车装运B种水果,根据下表提供的信息,求y与x之间的函数关系式并直接写出自变量x的取值范围;
| 水果品种 | A | B | C |
| 每辆汽车运装量/t | 4 | 3 | 2 |
| 每吨水果获利/百元 | 6 | 8 | 5 |
12.在一个不透明的盒子里,装有5个黑球和若干个白球,这些球除颜色外都相同,将其摇匀后从中随机摸出一个球,记下颜色后再把它放回盒子中,不断重复,共摸球40次,其中10次摸到黑球,请估计盒子中白球的个数是( )
| A. | 10个 | B. | 15个 | C. | 20个 | D. | 25个 |
17.下列命题中,真命题是( )
| A. | 若a>b,则a2>ab | B. | 若$\sqrt{(1-m)^{2}}$=m-1,则m≤1 | ||
| C. | 若a>b,则$\frac{1}{a}$<$\frac{1}{b}$ | D. | 已知a,b为实数,若a+b=1,则ab≤$\frac{1}{4}$ |
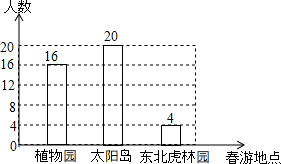 某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.
某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.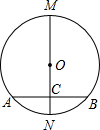 如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论:
如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论: 如图,C,D为线段AB上两点,且AC=BD,AE∥BF.AE=BF.求证:∠E=∠F.
如图,C,D为线段AB上两点,且AC=BD,AE∥BF.AE=BF.求证:∠E=∠F.