题目内容
函数y=-x2+px+q的图象与x轴交于(a,0),(b,0)两点,若a>1>b,则( )
| A、p+q>1 | B、p+q=1 |
| C、p+q<1 | D、pq>0 |
考点:抛物线与x轴的交点
专题:
分析:结合条件和二次函数图象可知当x=1时,对应的y值小于0,可得到关于p,q的关系式,可得到答案.
解答:解:
由题意可知a、b为方程-x2+px+q=0的两根,
∴4q-p2>0,
由 y=-x2+px+q的图象与x轴交于(a,0)和(b,0)且a>1>b得,当x=1时,y<0,
∴-12+p+q<0,
∴p+q<1,
故选C.
由题意可知a、b为方程-x2+px+q=0的两根,
∴4q-p2>0,
由 y=-x2+px+q的图象与x轴交于(a,0)和(b,0)且a>1>b得,当x=1时,y<0,
∴-12+p+q<0,
∴p+q<1,
故选C.
点评:本题主要考查二次函数与二次方程的关系,掌握二次函数图象在x=1时,对应的y<0是解题的关键,注意结合图形来理解.

练习册系列答案
相关题目
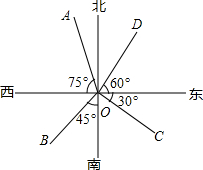 如图所示,对图中各射线表示的方向下列判断错误的是( )
如图所示,对图中各射线表示的方向下列判断错误的是( )| A、射线OA的方向是北偏西15° |
| B、射线OB的方向是南偏西45° |
| C、射线OC的方向是南偏东60° |
| D、射线OD的方向是北偏东60° |
 如图,已知∠AOB是直角,OM平分∠AOC,ON平分∠BOC,则∠MON的度数是( )
如图,已知∠AOB是直角,OM平分∠AOC,ON平分∠BOC,则∠MON的度数是( )| A、60° | B、50° |
| C、45° | D、30° |
 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.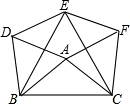 如图,以△ABC的三边为边,在BC边的同侧作等边△DBA,△EBC,△FAC.
如图,以△ABC的三边为边,在BC边的同侧作等边△DBA,△EBC,△FAC. 如图,OP是直角∠MON的平分线,以O为圆心,1为半径作
如图,OP是直角∠MON的平分线,以O为圆心,1为半径作
 点a,b在数轴上的位置如图,则a+b
点a,b在数轴上的位置如图,则a+b 如图,正比例函数y=kx(k>0)与反比例函数y=
如图,正比例函数y=kx(k>0)与反比例函数y=